Boog-samenhangende ruimten

Een topologische ruimte S heet boog-samenhangend wanneer je elk tweetal punten A en B met een continu pad kunt verbinden zonder de ruimte te verlaten.

Stel je een vel papier voor. We negeren even de randen alsof ze niet bestaan.

Dat vel stelt een open en ononderbroken vlak voor. Op zo'n vlak kun je met je pen van punt A naar punt B tekenen zonder dat je de pen hoeft op te tillen.

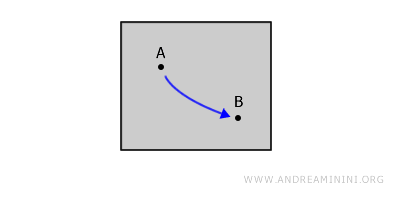
Het pad blijft volledig binnen het vlak. Dat is precies wat we bedoelen met een boog-samenhangende ruimte.

Elke boog-samenhangende ruimte is automatisch ook samenhangend.

Dat voelt logisch aan. Als een ruimte uit losse delen zou bestaan, kun je onmogelijk met één vloeiende lijn van het ene punt naar het andere gaan zonder die ruimte te verlaten.

Het omgekeerde is echter niet altijd waar. Niet elke samenhangende ruimte is ook boog-samenhangend.

Dat klinkt vreemd, maar er bestaan echte voorbeelden die dat laten zien. Laten we er één bekijken.

Neem twee verzamelingen, Q en T:

$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$

$$ T = \{ \ 0 \} $$

De verzameling Q bevat alle punten van de sinusfunctie sin(1/x) voor alle reële getallen behalve nul. Bij x=0 is de functie niet gedefinieerd, want delen door nul is niet mogelijk.

T bestaat slechts uit het punt nul zelf.

De twee verzamelingen Q en T liggen oneindig dicht bij elkaar, zoals goed te zien is in de grafiek van sin(1/x).

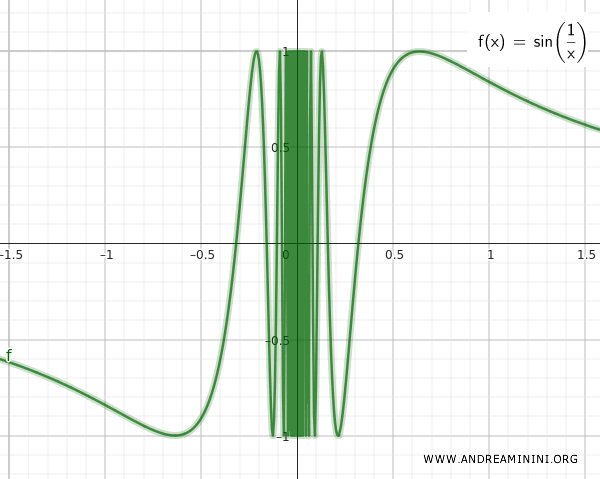
Wanneer we ze samen nemen, krijgen we de verzameling S:

$$ S = Q \cup T $$

Deze verzameling S is samenhangend. Rond nul kun je namelijk altijd een kleine omgeving (0-ε, 0+ε) vinden waarin punten van Q voorkomen.

Dat komt doordat nul een accumulatiepunt is van de functie sin(1/x). De waarden van de functie blijven in de buurt van nul heen en weer oscilleren zonder zich ooit echt los te maken.

Maar S is niet boog-samenhangend. Er bestaat geen continu pad dat een punt van Q met nul (de verzameling T) kan verbinden.

Opmerking: Bij de functie f(x)=1/x is dat anders. Daar zijn Q en T duidelijk gescheiden en liggen ze niet oneindig dicht bij elkaar.

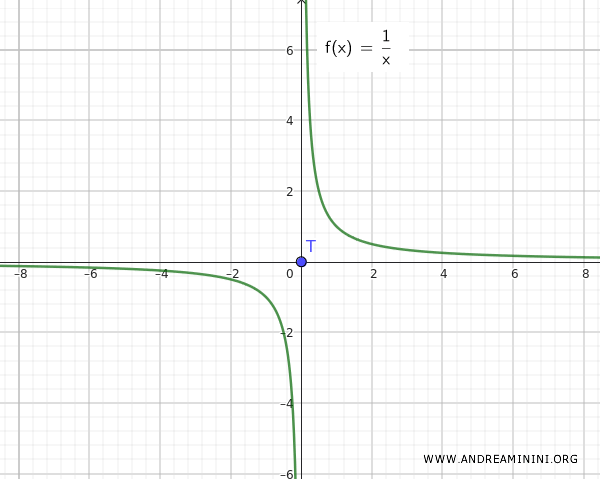
Dit voorbeeld laat zien dat het samenvoegen van een samenhangende verzameling Q={∀ x ∈ R-{0}, 1/x} met een geïsoleerd punt T={0} niet automatisch tot een samenhangende ruimte leidt, behalve als dat punt zelf ook een accumulatiepunt is.

 Enzovoort.