Samenhang in de topologie

In de topologie noemen we een ruimte samenhangend wanneer zij niet kan worden opgesplitst in twee afzonderlijke open deelverzamelingen. Met andere woorden: samenhang beschrijft of een ruimte als één ondeelbaar geheel kan worden beschouwd, zonder interne scheidingen die haar uiteentrekken.

Samenhang vertelt ons hoe de verschillende delen van een topologische ruimte met elkaar verbonden zijn, of juist van elkaar gescheiden blijven.

Het gaat om een zuiver topologische eigenschap, omdat zij volledig wordt gedefinieerd in termen van open verzamelingen.

Daarom behoort samenhang tot de kernbegrippen van de topologie, naast fundamentele noties zoals continuïteit.

In veel takken van de wiskunde speelt samenhang een centrale rol. Zij helpt wiskundigen de globale structuur van ruimten te begrijpen en te analyseren, en maakt het mogelijk om verschillende soorten ruimten te classificeren op basis van hun interne samenstelling.

Een praktisch voorbeeld

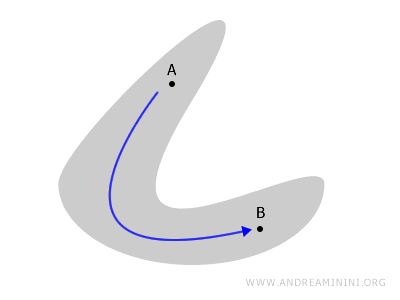
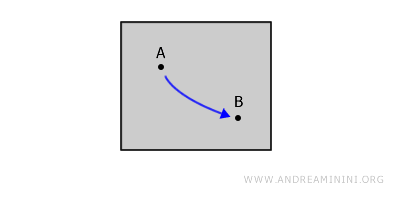
Stel je een figuur in het vlak of een lichaam in de ruimte voor. We spreken van een samenhangende ruimte wanneer je tussen twee willekeurige punten A en B altijd een continu pad kunt tekenen dat volledig binnen de ruimte blijft.

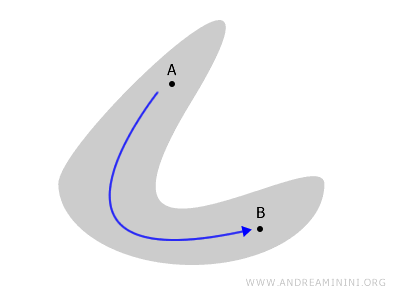
Wanneer bepaalde delen van de ruimte echter van elkaar geïsoleerd zijn, noemen we de ruimte niet-samenhangend.

In het onderstaande voorbeeld bestaat de ruimte uit twee losse componenten. Elk pad dat de punten A en B zou moeten verbinden, zou de ruimte moeten verlaten, wat volgens de definitie niet is toegestaan.

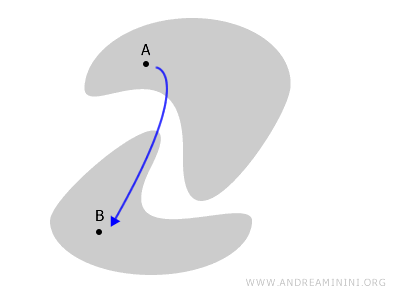
Om dit idee concreter te maken, bekijken we een alledaags voorbeeld.

Wanneer spreken we van een niet-samenhangende ruimte?

Denk aan twee kamers in hetzelfde gebouw, gescheiden door een muur. Elke kamer vormt een open ruimte zonder de muren zelf, want grenzen behoren niet tot open verzamelingen. De twee kamers zijn dus afzonderlijke open deelverzamelingen.

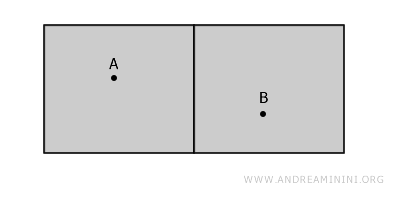
Ze lijken verbonden, maar dat zijn ze niet. Elk traject van punt A naar punt B zou door de muur moeten gaan, en die behoort niet tot de ruimte.

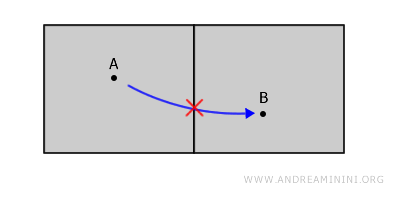
Belangrijk om te onthouden: grenzen maken geen deel uit van open verzamelingen.

Lokale samenhang

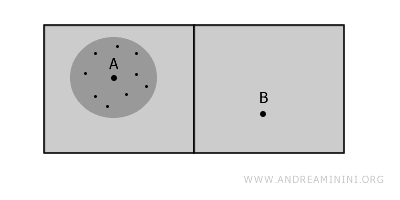
Een ruimte heet lokaal samenhangend wanneer elk punt een open omgeving bezit die zelf samenhangend is, ook als de ruimte als geheel dat niet is. Met andere woorden: in de onmiddellijke nabijheid van elk punt vormt de ruimte één samenhangend geheel.

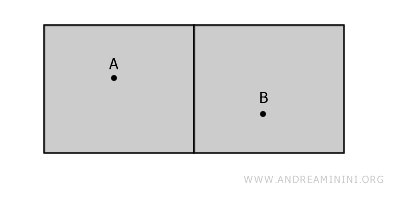
Neem opnieuw het voorbeeld van de twee kamers. Hoewel zij samen geen samenhangende ruimte vormen, is elke kamer op zichzelf lokaal samenhangend: binnen één kamer kun je van elk punt naar elk ander punt gaan zonder de ruimte te verlaten.

Bij punt A bestaat dus een kleine open omgeving waarin alle punten onderling verbonden zijn, wat lokale samenhang illustreert.

Hetzelfde geldt voor punt B, dat eveneens een lokaal samenhangende omgeving heeft.

Vormen van samenhang

In de topologie onderscheidt men verschillende vormen van samenhang. De belangrijkste zijn:

• Topologische samenhang
  Een topologische ruimte \( X \) heet samenhangend wanneer zij niet kan worden opgesplitst in twee open, niet-lege en disjuncte deelverzamelingen waarvan de vereniging de volledige ruimte vormt. Met andere woorden, de ruimte laat geen scheiding toe in twee onafhankelijke delen.

  Voorbeeld. De ruimte \((-1,1)\) is samenhangend, terwijl de ruimte \((-1,0)\cup(0,1)\) dat niet is. In dit geval bestaan er twee open, disjuncte en niet-lege verzamelingen, namelijk \((-1,0)\) en \((0,1)\), waarvan de vereniging de volledige ruimte vormt. Deze twee verzamelingen vormen samen een scheiding van de ruimte.

• Pad-samenhang (of boogsamenhang)
  Een topologische ruimte heet pad-samenhangend wanneer voor elk paar punten A en B een continu pad bestaat dat deze punten verbindt en volledig binnen de ruimte blijft. Elke pad-samenhangende ruimte is samenhangend, maar het omgekeerde geldt niet in het algemeen.

  Denk aan een gesloten figuur in het vlak. Voor elk paar punten A en B binnen de figuur kan men een continue kromme tekenen die beide punten verbindt, zonder de figuur te verlaten.
  
  Verschil tussen boog- en pad-samenhang.  Bij boogsamenhang moet het pad bovendien injectief zijn, wat betekent dat het zichzelf niet mag snijden en geen punt meer dan eenmaal mag passeren.

• Eenvoudige samenhang
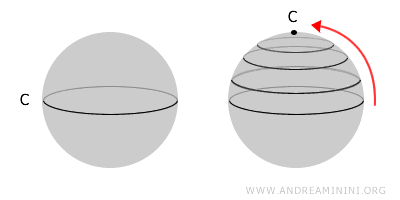
  Een ruimte heet eenvoudig samenhangend wanneer elke gesloten lus in de ruimte kan worden samengetrokken tot één enkel punt. Dit betekent dat de ruimte geen gaten of holtes bevat. Elke eenvoudig samenhangende ruimte is samenhangend, maar niet elke samenhangende ruimte is eenvoudig samenhangend. In formele termen is elke lus homotoop aan een punt.

  Een bol vormt het klassieke voorbeeld: elke lus op het oppervlak kan worden verkleind tot één punt. Een torus daarentegen bezit een opening, waardoor niet elke lus kan worden samengetrokken. Zo'n ruimte is samenhangend, maar niet eenvoudig samenhangend.
  
  
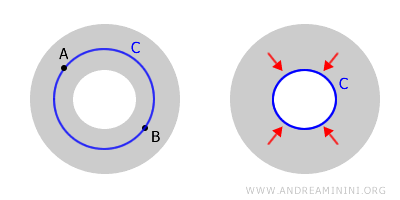
  Dergelijke ruimten noemt men meervoudig samenhangend. Ringvormige structuren zijn typische voorbeelden.

Tot slot

Samenhang is een ogenschijnlijk eenvoudig begrip met diepe gevolgen. Het helpt ons precies te formuleren wat het betekent dat een ruimte "één geheel" vormt. In de reële getallen bijvoorbeeld zijn precies de intervallen samenhangend. Dit illustreert hoe abstracte topologische ideeën tot verrassend concrete inzichten leiden.