Scheiding van een deelverzameling door open verzamelingen

Zij $ A $ een deelverzameling van een topologische ruimte $ X $. Een fundamentele vraag is wanneer zo'n verzameling werkelijk uiteenvalt in twee afzonderlijke delen. In de topologie wordt dit beschreven met behulp van twee open verzamelingen, $ U $ en $ V $, die samen vastleggen hoe $ A $ wordt opgesplitst. Men spreekt van een scheiding van $ A $ zodra aan de volgende drie klassieke voorwaarden is voldaan:

De twee open verzamelingen overdekken $ A $ volledig \[ A \subseteq U \cup V \]
Beide open verzamelingen snijden $ A $ in ten minste één punt \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
Geen enkel punt van $ A $ behoort tegelijkertijd tot beide verzamelingen \[ U \cap V \cap A = \varnothing \]

Wanneer deze drie voorwaarden gelijktijdig vervuld zijn, ontstaat een helder beeld. De deelverzameling $ A $ valt uiteen in twee delen die elkaar nergens raken. Het ene deel ligt volledig binnen $ U $, het andere volledig binnen $ V $. Precies dit idee vormt de kern van wat men in de topologie een scheiding noemt.

Deze benadering is een van de meest directe en gebruikte manieren om vast te stellen of een deelverzameling van een topologische ruimte werkelijk gescheiden is.

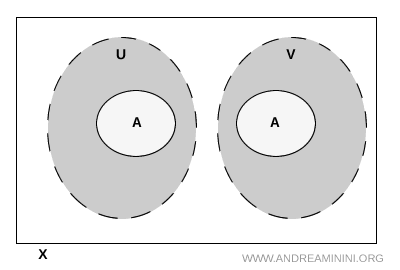
schematische voorstelling van een deelverzameling die door twee open verzamelingen wordt gescheiden

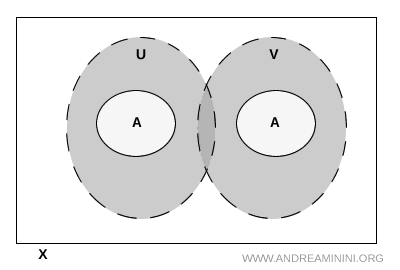
Nota. De open verzamelingen $ U $ en $ V $ mogen elkaar buiten $ A $ best snijden. Dat heeft geen invloed op de scheiding, zolang deze doorsnede maar geen punten van $ A $ bevat. Voor het begrip scheiding is uitsluitend van belang hoe beide verzamelingen zich ten opzichte van $ A $ gedragen.
voorbeeld waarin twee open verzamelingen elkaar buiten A snijden zonder de scheiding te beïnvloeden

Concreet voorbeeld

Een concreet voorbeeld maakt dit begrip onmiddellijk inzichtelijk. Neem $ X = \mathbb{R} $ met de gebruikelijke topologie en beschouw de deelverzameling

$$ A = [-2,-1] \cup [1,2] $$

Deze twee gesloten intervallen liggen duidelijk los van elkaar.

Kies nu de open verzamelingen

$$ U = (-3,0) $$

$$ V = (0,3) $$

Op de reële lijn zien deze verzamelingen er als volgt uit:

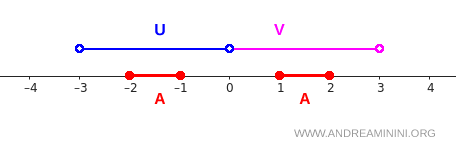
reële lijn met de open verzamelingen U en V en de twee gescheiden delen van A

Het interval $ [-2,-1] $ ligt volledig in $ U $, terwijl het interval $ [1,2] $ volledig in $ V $ ligt. De controle van de voorwaarden verloopt dan rechtstreeks:

1. De deelverzameling $ A $ is geheel opgenomen in de unie van $ U $ en $ V $:

$$ A \subseteq U \cup V $$

2. Beide open verzamelingen snijden $ A $:

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

3. Geen enkel punt van $ A $ behoort tot beide verzamelingen tegelijk:

$$ U \cap V \cap A = \varnothing $$

Hieruit volgt dat $ U $ en $ V $ de deelverzameling $ A $ daadwerkelijk scheiden in $ X $. Omdat $ A $ uit twee gescheiden componenten bestaat, laat dit voorbeeld op een bijzonder duidelijke manier zien hoe het abstracte begrip scheiding zich in een concreet geval manifesteert.