Stelling: karakterisering van samenhangende ruimten aan de hand van open en gesloten verzamelingen
Een topologische ruimte \( X \) heet samenhangend als en slechts als de enige deelverzamelingen van \( X \) die zowel open als gesloten zijn (ook wel clopen genoemd) het geheel \( X \) zelf en de lege verzameling \( \emptyset \) zijn.
Met andere woorden: een ruimte is samenhangend wanneer ze niet kan worden opgesplitst in twee gescheiden open verzamelingen die allebei niet leeg zijn. In dat geval blijven alleen de twee triviale clopen verzamelingen over: de hele ruimte en de lege verzameling.
Dit principe vormt een van de basisideeën van de topologische samenhang. Het laat zien hoe je kunt bepalen of een ruimte samenhangend is, zonder dat je ingewikkeldere begrippen zoals pad-samenhang hoeft te gebruiken.
Hoe kun je dat interpreteren?
Een deelverzameling die tegelijk open en gesloten is, zorgt in feite voor een scheiding in de ruimte. Ze verdeelt \( X \) in twee open verzamelingen die elkaar niet overlappen en die allebei punten bevatten.
Als zo'n scheiding mogelijk is, kan de ruimte worden geschreven als de unie van twee gescheiden open verzamelingen. In dat geval is de ruimte niet samenhangend (of onsamenhangend).
Maar als de enige clopen verzamelingen van \( X \) het geheel \( X \) en de lege verzameling \( \emptyset \) zijn, bestaat er geen enkele scheiding. Dan is \( X \) per definitie samenhangend.
Opmerking. In elke topologische ruimte zijn zowel de volledige verzameling \( X \) als de lege verzameling \( \emptyset \) altijd tegelijk open en gesloten. Dat zijn de twee triviale clopen verzamelingen.
Voorbeeld 1: een eindige ruimte die niet samenhangend is
Neem \( X = \{ a, b, c, d \} \) met de topologie \( T \), waarin de open verzamelingen zijn: \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \} \) en \( \emptyset \).
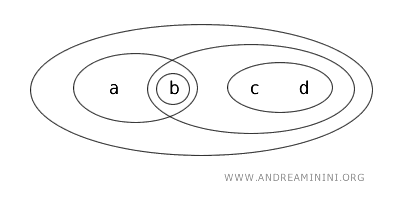
Hier is de verzameling \( \{ a, b \} \) clopen, omdat ze aan beide voorwaarden voldoet:
- ze is open, omdat ze expliciet voorkomt in de familie van open verzamelingen van \( T \);
- ze is gesloten, omdat haar complement \( X \setminus \{ a, b \} = \{ c, d \} \) ook open is in \( T \).
Daaruit volgt dat de topologische ruimte \( (X, T) \) niet samenhangend is: ze bevat namelijk een niet-lege, eigen deelverzameling die clopen is.
Het bestaan van één niet-triviale clopen verzameling is genoeg om te bewijzen dat een ruimte niet samenhangend is. Zo'n verzameling laat zien dat de ruimte kan worden opgesplitst in twee gescheiden open verzamelingen, \( \{ a, b \} \) en \( \{ c, d \} \). Daarmee is de voorwaarde voor topologische samenhang niet vervuld.
Voorbeeld 2: de reële rechte
Beschouw de verzameling van reële getallen \( \mathbb{R} \), uitgerust met de standaardtopologie, die wordt bepaald door de open intervallen \( (a, b) \).
In deze topologie zijn de intervallen \( (a, b) \) open maar niet gesloten, terwijl de intervallen \( [a, b] \) gesloten maar niet open zijn.
De enige verzamelingen in \( \mathbb{R} \) die tegelijk open en gesloten zijn, zijn \( \mathbb{R} \) zelf en de lege verzameling \( \emptyset \).
Daaruit volgt dat de reële rechte met de standaardtopologie een samenhangende ruimte is.
Voorbeeld 3: een niet-samenhangende deelruimte van \( \mathbb{R} \)
Neem nu de deelruimte \( X = (0,1) \cup (2,3) \subset \mathbb{R} \), uitgerust met de subruimtetopologie (geïnduceerde topologie) van \( \mathbb{R} \).
In dit geval zijn de intervallen \( (0,1) \) en \( (2,3) \) beide open én gesloten in \( X \). Dat komt doordat het complement van elk precies het andere interval is. Concreet:
- het complement van \( (0,1) \) in \( X \) is \( (2,3) \), dat open is in \( X \);
- het complement van \( (2,3) \) in \( X \) is \( (0,1) \), dat eveneens open is in \( X \).
Beide deelverzamelingen zijn dus clopen.
Aangezien \( X \) niet-triviale verzamelingen bevat die tegelijk open en gesloten zijn, is \( X \) niet samenhangend.
We kunnen \( X \) zien als opgebouwd uit twee afzonderlijke samenhangende componenten: \( (0,1) \) en \( (2,3) \). Ze zijn open, disjunct en niet leeg. Dat er geen topologische verbinding bestaat tussen punten van het ene interval en die van het andere, maakt precies duidelijk waarom deze ruimte onsamenhangend is.