Samenhang via een gemeenschappelijke doorsnede
Laat \( C_1, C_2, \dots, C_n \subset X \) samenhangende deelverzamelingen zijn van een topologische ruimte \( X \), met als eigenschap dat hun doorsnede niet leeg is: \[
\bigcap_{i=1}^n C_i \neq \varnothing . \] Dan is ook hun vereniging \( \bigcup_{i=1}^n C_i \) een samenhangende verzameling.
Met andere woorden: zodra meerdere samenhangende verzamelingen minstens één punt delen, vormen zij samen opnieuw één samenhangend geheel.
Dit idee is eenvoudig maar fundamenteel. Een gemeenschappelijk punt verhindert namelijk dat de totale verzameling in afzonderlijke, losstaande delen uiteenvalt.
Opmerking. De voorwaarde \( \bigcap_{i=1}^n C_i \neq \varnothing \) is voldoende om de samenhang van de vereniging \( \bigcup_{i=1}^n C_i \) te garanderen, maar zij is niet noodzakelijk. Een vereniging van samenhangende verzamelingen kan ook samenhangend blijven zonder één enkel gemeenschappelijk punt, bijvoorbeeld wanneer de verzamelingen elkaar trapsgewijs of kettingvormig overlappen.
Een concreet voorbeeld
Beschouw de volgende deelverzamelingen van \( \mathbb{R}^2 \):
- \( C_1 \): het horizontale lijnstuk van \( (-1,0) \) tot \( (1,0) \)
- \( C_2 \): het verticale lijnstuk van \( (0,-1) \) tot \( (0,1) \)
- \( C_3 \): het diagonale lijnstuk van \( (-1,-1) \) tot \( (1,1) \)
Elk van deze verzamelingen is samenhangend.
Bovendien hebben ze één punt gemeen, namelijk \( (0,0) \):
\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]
De doorsnede is dus niet leeg:
\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]
Volgens het bovenstaande criterium is hun vereniging daarom samenhangend:
\[ C_1 \cup C_2 \cup C_3 \]
De drie lijnstukken komen samen in één centraal punt, wat ervoor zorgt dat de volledige figuur samenhangend blijft.
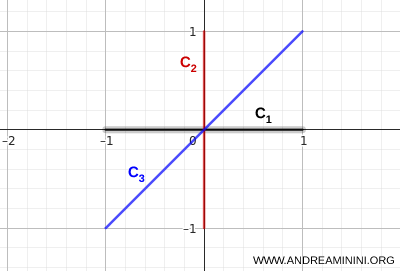
Vanuit elk punt op een van de lijnstukken kan men elk ander punt bereiken zonder de verzameling te verlaten.
Opmerking. Er bestaan ook andere criteria voor samenhang die niet gebaseerd zijn op het bestaan van één gemeenschappelijk punt. Zo blijft de vereniging \( \bigcup_i C_i \) samenhangend wanneer de verzamelingen \( C_i \) elkaar opeenvolgend snijden, dat wil zeggen wanneer \( C_i \cap C_{i+1} \neq \varnothing \). In dat geval kan de totale doorsnede leeg zijn, \( \bigcap_i C_i = \varnothing \), terwijl de vereniging toch samenhangend blijft. Dit is bijvoorbeeld het geval bij drie lijnstukken die samen een driehoek vormen. Hoewel zij geen enkel gemeenschappelijk punt delen, blijft hun vereniging samenhangend.
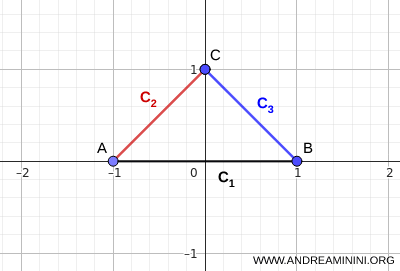
Dit voorbeeld laat zien dat samenhang kan ontstaan door een aaneenschakeling van lokale overlappingen.
Bewijs
Zij \( X \) een topologische ruimte en \( \{C_i\}_{i \in I} \) een familie van samenhangende deelverzamelingen van \( X \) waarvoor geldt:
\[ \bigcap_{i \in I} C_i \neq \varnothing \]
Veronderstel, ter tegenspraak, dat de vereniging
\[ C = \bigcup_{i \in I} C_i \]
niet samenhangend is.
Dan bestaan er twee open verzamelingen \( U \) en \( V \) die samen een scheiding van \( C \) vormen:
- \( U \cap C \neq \varnothing \)
- \( V \cap C \neq \varnothing \)
- \( (U \cap C) \cap (V \cap C) = \varnothing \)
- \( C = (U \cap C) \cup (V \cap C) \)
Omdat de doorsnede van alle verzamelingen \( C_i \) niet leeg is, bestaat er een punt
\[ x \in \bigcap_{i \in I} C_i \]
Dit punt behoort dus tot elk van de verzamelingen \( C_i \), en in het bijzonder tot \( C \). Het moet daarom in \( U \) of in \( V \) liggen, maar niet in beide, aangezien deze samen een scheiding van \( C \) vormen. Zonder verlies aan algemeenheid nemen we aan dat
\[ x \in U \quad \text{en} \quad x \notin V \]
Aangezien elk \( C_i \subset C \), geldt:
\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]
De verzamelingen \( C_i \cap U \) en \( C_i \cap V \) zijn open in de geïnduceerde topologie op \( C_i \), onderling disjunct, en samen gelijk aan \( C_i \). Omdat elk \( C_i \) samenhangend is, moet één van beide leeg zijn.
Daaruit volgt dat elk \( C_i \) volledig in \( U \) of volledig in \( V \) ligt.
Aangezien \( x \in C_i \) en \( x \in U \), kan geen enkel \( C_i \) volledig in \( V \) liggen. Dus geldt:
\[ C_i \subset U \quad \text{voor alle } i \in I \]
Daaruit volgt dat ook de volledige vereniging in \( U \) ligt:
\[ \bigcup_{i \in I} C_i \subset U \]
Dit staat in tegenspraak met de aanname dat \( V \cap C \neq \varnothing \).
De tegenspraak toont aan dat de oorspronkelijke veronderstelling onjuist was. We concluderen dus dat de vereniging \( \bigcup_{i \in I} C_i \) een samenhangende verzameling is.
En zo verder.