Samenhang in de topologie
Wat betekent "samenhangend" precies?
Een topologische ruimte \( X \) noemen we samenhangend als zij niet kan worden opgesplitst in twee open deelverzamelingen die beide niet leeg zijn, geen enkel punt gemeen hebben en samen de volledige ruimte vormen.
- \( U \neq \emptyset \) en \( V \neq \emptyset \) - beide verzamelingen bevatten minstens één punt;
- \( U \cap V = \emptyset \) - zij overlappen elkaar niet;
- \( U \cup V = X \) - samen bedekken zij de hele ruimte.
Bestaat er zo'n paar open verzamelingen, dan zeggen we dat de ruimte niet-samenhangend is.
Met andere woorden: een ruimte is topologisch samenhangend wanneer zij niet kan worden uiteengerafeld in twee gescheiden open delen die samen alles omvatten. Als dat wel mogelijk is, spreken we van een scheiding van \( X \).
Opmerking. Dit is de formele definitie van topologische samenhang. Later zal blijken dat dit begrip verschilt van pad-samenhang (of boog-samenhang). Deze twee begrippen vallen niet altijd samen.
Een concreet voorbeeld
We bekijken een eenvoudig, maar verhelderend voorbeeld. Neem een verzameling met drie elementen
$$ X = \{ a, b, c \} $$
en definieer daarop twee verschillende topologieën:
- Topologie A
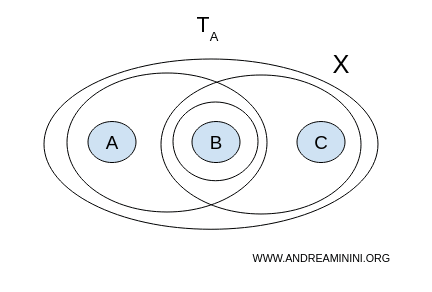
$$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$ - Topologie B
$$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$
De vraag is: welke van deze twee topologische ruimten is samenhangend?
1. Topologie A
We onderzoeken of er twee niet-lege, disjuncte open verzamelingen bestaan die samen \( X \) bedekken. In deze topologie geldt:
- \( U = \{a,b\}, V = \{b,c\} \) hebben het punt \( b \) gemeen en zijn dus niet disjunct;
- \( U = \{a,b\}, V = \{b\} \) overlappen elkaar;
- \( U = \{b\}, V = \{b,c\} \) overlappen eveneens.
Er bestaat dus geen enkel paar open verzamelingen dat aan alle voorwaarden voldoet. De ruimte met topologie A is daarom samenhangend.
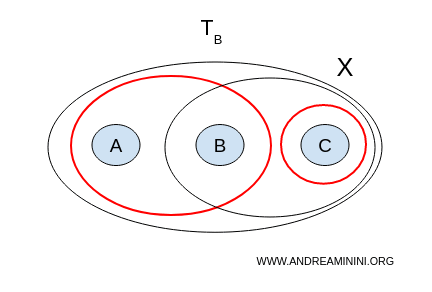
2. Topologie B
We voeren hetzelfde onderzoek uit voor de tweede topologie:
- \( U = \{a,b\}, V = \{b,c\} \) zijn niet disjunct, omdat zij beide het punt \( b \) bevatten;
- \( U = \{a,b\}, V = \{c\} \) zijn niet-lege, disjuncte open verzamelingen en hun vereniging is precies \( X \).
Het paar \( (U = \{a,b\}, V = \{c\}) \) vormt dus een scheiding van de ruimte. De ruimte met topologie B is daarom niet-samenhangend.
Opmerking. Dit voorbeeld laat zien dat samenhang niet alleen afhangt van de onderliggende verzameling, maar wezenlijk van de gekozen topologie. Met exact dezelfde punten kunnen verschillende topologieën tot totaal verschillende globale eigenschappen leiden.
Een tweede voorbeeld: de reële lijn zonder één punt
Neem de reële getallenlijn en verwijder één enkel punt \( n \), bijvoorbeeld \( n = 0 \):
$$ X = (-\infty, n) \cup (n, +\infty) $$
Of, equivalent:
$$ X = \mathbb{R} \setminus \{n\} $$
Is deze ruimte nog samenhangend?
Beschouw de verzamelingen \( U = (-\infty, n) \) en \( V = (n, +\infty) \). Deze zijn:
- open in de gebruikelijke topologie op \( \mathbb{R} \);
- disjunct, zij hebben geen enkel punt gemeen;
- beide niet leeg.
Hun vereniging is precies \( X \). Zij vormen dus een scheiding van de ruimte.
Daarom is de ruimte \( X = \mathbb{R} \setminus \{n\} \) niet-samenhangend: zij valt uiteen in twee open delen die niets gemeen hebben maar samen alles bedekken.
Opmerking. Het verwijderen van één enkel punt "breekt" de reële lijn. De ruimte splitst zich in een linker- en een rechterdeel, die niet meer via een continu pad met elkaar verbonden kunnen worden. De ruimte is dus zowel niet-samenhangend als niet pad-samenhangend.
Samenhang en pad-samenhang: wat is het verschil?
De begrippen samenhang en pad-samenhang liggen dicht bij elkaar, maar zijn niet equivalent.
- Topologische samenhang
De ruimte kan niet worden opgesplitst in twee disjuncte, niet-lege open deelverzamelingen. - Pad-samenhang
Voor elk paar punten in de ruimte bestaat een continu pad dat deze punten verbindt en volledig binnen de ruimte blijft. Is dit pad bovendien injectief, dan spreekt men van boog-samenhang.
Belangrijk is het volgende:
Elke pad-samenhangende ruimte is samenhangend, maar niet elke samenhangende ruimte is pad-samenhangend.
Een continu pad verhindert immers dat de ruimte in twee open delen kan worden gesplitst. Het omgekeerde geldt echter niet: sommige ruimten zijn wel samenhangend, maar laten geen continu pad toe tussen willekeurige punten.
Voorbeeld. Een klassiek voorbeeld is de sinuskromme van de topoloog:
$$ S = \{ (x, \sin(1/x)) \mid x > 0 \} \cup \{ (0, y) \mid -1 \le y \le 1 \} $$
Deze ruimte is samenhangend, omdat zij niet kan worden gescheiden door open verzamelingen, maar zij is niet pad-samenhangend. Er bestaat geen continu pad dat een punt op de oscillerende kromme verbindt met een punt op het verticale segment.
Dit voorbeeld toont hoe subtiel het begrip samenhang kan zijn in de topologie: een klein structureel detail kan het verschil maken tussen één geheel en een ruimte die geen paden toelaat.
Notities
Verdere opmerkingen over samenhangende ruimten:
- Stelling: karakterisering van samenhangende ruimten aan de hand van open en gesloten (clopen) verzamelingen
Een topologische ruimte \( X \) is samenhangend dan en slechts dan als de enige deelverzamelingen van \( X \) die zowel open als gesloten zijn, het geheel \( X \) zelf en de lege verzameling \( \emptyset \) zijn.
En zo verder.