Elke samenhangende deelverzameling is vervat in precies één samenhangende component
Laat \( A \) en \( B \) twee deelverzamelingen zijn van een topologische ruimte \( X \). We nemen aan dat \( A \) samenhangend is en dat \( A \subset B \). Kan de verzameling \( B \) in \( X \) worden gescheiden in twee deelverzamelingen \( B_1 \) en \( B_2 \), dan moet \( A \) volledig in één van beide liggen: $$ A \subset B_1 \quad \text{of} \quad A \subset B_2 $$
In eenvoudige woorden: een samenhangende deelverzameling kan niet tegelijk beide delen van een scheiding raken.
Zodra een samenhangende deelverzameling deel uitmaakt van een verzameling die uiteenvalt in twee onderling disjuncte delen, kan zij zich niet over die twee verdelen. Zij blijft noodzakelijk binnen één enkel deel.
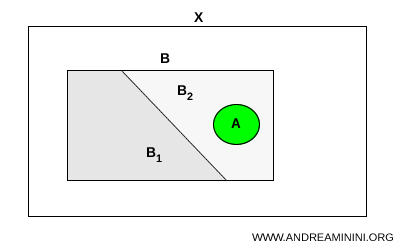
Een intuïtief beeld helpt. Denk aan een samenhangende deelverzameling als aan een ononderbroken koord in een envelop. Wordt de envelop verdeeld in twee gescheiden vakken terwijl het koord intact blijft, dan kan het koord slechts in één van die vakken liggen. Om beide vakken tegelijk te bereiken, zou het koord moeten worden doorgesneden. Samenhang drukt precies deze onmogelijkheid uit om een verzameling "door te snijden" via een scheiding.
Een concreet voorbeeld
Beschouw de volgende topologische ruimte:
$$ X = \mathbb{R} $$
en de deelverzameling:
$$ B = (-3,4) $$
Deze verzameling kan op natuurlijke wijze worden gescheiden in:
$$ B_1 = (-3,0) $$
$$ B_2 = (0,4) $$
De twee deelverzamelingen zijn onderling disjunct:
$$ B_1 \cap B_2 = \varnothing $$
en hun vereniging levert precies \( B \) op:
$$ B_1 \cup B_2 = B $$
Bovendien zijn \( B_1 \) en \( B_2 \) open in de deelruimtetopologie op \( B \). Zij vormen dus een geldige scheiding van \( B \) in \( X \).
Neem nu een samenhangende deelverzameling van \( B \):
$$ A = (1,2) $$
Dan geldt duidelijk \( A \subset B_2 \). De deelverzameling \( A \) ligt volledig in één van de twee delen van de scheiding, precies zoals het algemene resultaat voorspelt.
Opmerking. Kiezen we daarentegen \( A = (-1,1) \), dan geldt $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ Dit is onmogelijk, omdat \( B_1 \) en \( B_2 \) samen een scheiding van \( B \) vormen. Een samenhangende deelverzameling van \( B \) kan zich niet over beide delen uitstrekken. Als dat wel zo zou zijn, dan zou \( A \) zelf gescheiden zijn, in tegenspraak met het fundamentele feit dat het interval \( (-1,1) \) samenhangend is. Het probleem zit dus niet in een verlies van samenhang van \( (-1,1) \), maar in de onmogelijkheid om dit interval onder te brengen in een op deze manier gescheiden verzameling.
Bewijs
Hypothesen
Laat \( A \) en \( B \) deelverzamelingen zijn van een topologische ruimte \( X \):
$$ A \subset X \quad \text{en} \quad B \subset X $$
We nemen aan dat:
- \( A \) samenhangend is
- \( A \subset B \)
- \( B_1 \) en \( B_2 \) een scheiding van \( B \) vormen in \( X \)
Stelling
Onder deze aannames geldt:
$$ A \subset B_1 \quad \text{of} \quad A \subset B_2 $$
Bewijs
Omdat \( B_1 \) en \( B_2 \) een scheiding van \( B \) vormen, geldt:
- \( B_1 \cap B_2 = \varnothing \)
- \( B = B_1 \cup B_2 \)
- \( B_1 \) en \( B_2 \) zijn open in de deelruimtetopologie op \( B \)
Stel nu, om een tegenspraak te verkrijgen, dat \( A \) noch volledig in \( B_1 \), noch volledig in \( B_2 \) ligt. Dan:
$$ A \cap B_1 \neq \varnothing \qquad \text{en} \qquad A \cap B_2 \neq \varnothing $$
Aangezien \( A \subset B \), volgt:
$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$
De verzamelingen \( A \cap B_1 \) en \( A \cap B_2 \) zijn disjunct. Bovendien zijn zij open in de deelruimtetopologie op \( A \), omdat \( B_1 \) en \( B_2 \) open zijn in \( B \).
We hebben dus twee niet-lege, open en disjuncte deelverzamelingen van \( A \) die samen \( A \) vormen. Dit is een scheiding van \( A \), wat in tegenspraak is met de samenhang van \( A \).
De veronderstelling leidt dus tot een contradictie. Bijgevolg moet gelden:
$$ A \subset B_1 \quad \text{of} \quad A \subset B_2 $$
De stelling is hiermee bewezen.
En zo verder.