Eenvoudig samenhangende ruimten in de topologie
Een topologische ruimte heet eenvoudig samenhangend als elke gesloten kromme in die ruimte continu kan worden vervormd tot één enkel punt, zonder de ruimte te verlaten.
Met andere woorden: elke lus binnen de ruimte kan worden "ingetrokken" tot een punt, zolang we maar binnen diezelfde ruimte blijven. Er is dus geen enkel obstakel dat de samentrekking verhindert.
Zo'n ruimte vormt één geheel en bevat geen interne "gaten". Ze is dus niet alleen samenhangend, maar ook vrij van topologische hindernissen.
Opmerking: elke eenvoudig samenhangende ruimte is samenhangend, maar niet elke samenhangende ruimte is eenvoudig samenhangend. De tweede eigenschap is strenger en zegt meer over de structuur van de ruimte zelf.
Een duidelijk voorbeeld
Neem bijvoorbeeld een sfeer. Dit is een typisch voorbeeld van een eenvoudig samenhangende ruimte: elke gesloten kromme op het oppervlak kan geleidelijk worden samengedrukt tot één enkel punt, zonder de sfeer te verlaten.
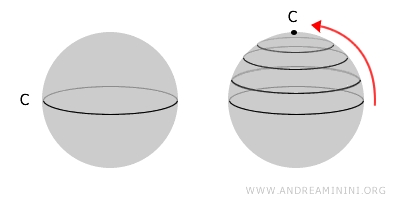
Een torus - beter bekend als een "donut" - vormt daarentegen een ruimte die niet eenvoudig samenhangend is. Het centrale gat verhindert dat bepaalde lussen volledig tot een punt kunnen worden teruggebracht.
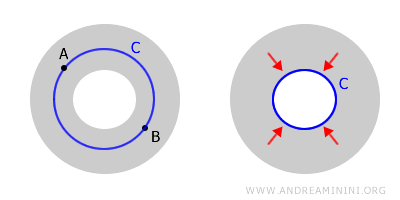
Dit voorbeeld laat zien dat een ruimte wel samenhangend kan zijn, zonder eenvoudig samenhangend te zijn. In een torus kun je immers elk tweetal punten, A en B, met een pad verbinden dat binnen de ruimte blijft. Toch kun je niet elke lus tot één punt vervormen - het gat blijft altijd in de weg.
Wanneer een ruimte samenhangend is, maar niet eenvoudig samenhangend, spreken wiskundigen van een meervoudig samenhangende ruimte. Voorbeelden hiervan zijn een ringvormig gebied of een torus.
Samenvattend: eenvoudige samenhang gaat een stap verder dan gewone of pad-samenhang. Ze zegt niet alleen dat de ruimte één geheel vormt, maar ook dat ze geen topologische obstakels bevat die lussen verhinderen om tot een punt te worden samengedrukt.