Topologie

Topologie is een bijzondere tak van de wiskunde die onderzoekt wat er met vormen en ruimten gebeurt als je ze uitrekt, buigt of vervormt - zolang je ze maar niet scheurt of aan elkaar plakt. Ze kijkt dus niet naar afstanden of hoeken, maar naar de diepere structuur van objecten: hoe alles met elkaar verbonden blijft.

Je kunt het zien als een manier om te begrijpen wat er écht hetzelfde blijft, zelfs als een vorm drastisch verandert. Een koffiekop en een donut lijken totaal verschillend, maar topologisch gezien zijn ze identiek: ze hebben allebei één gat.

Topologie draait om één kernidee: de topologische ruimte. Dat is een verzameling punten met een structuur die beschrijft wat ‘nabijheid’ of ‘continuïteit’ betekent, zonder dat we daar getallen voor nodig hebben. De belangrijkste transformaties heten homeomorfismen - continue vervormingen die de topologische eigenschappen behouden.

Omdat ze objecten behandelt alsof ze van rubber zijn, wordt topologie ook wel de "rubbergeometrie" genoemd. Ze is een van de fundamenten van de moderne wiskunde en speelt een rol van kosmologie tot data-analyse.

Een beetje geschiedenis

Het verhaal van de topologie begint in de achttiende eeuw, met een vraag die ogenschijnlijk niets met wiskunde te maken had: het bruggenprobleem van Königsberg.

Leonhard Euler vroeg zich af of het mogelijk was door de stad te wandelen en daarbij alle zeven bruggen precies één keer over te steken. Het bleek onmogelijk - en dat simpele inzicht legde de basis voor de moderne topologie en de netwerktheorie.

Het bruggenraadsel: op een eiland in de rivier de Pregel liggen zeven bruggen. Kun je een route vinden die elke brug precies één keer gebruikt?

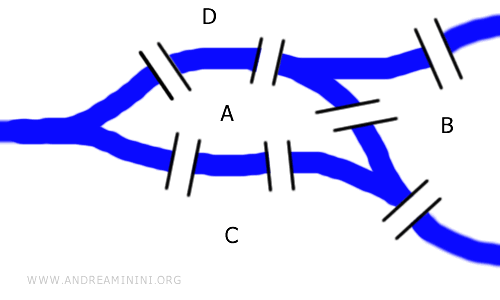
Het bijzondere is dat afstanden of lengtes er niet toe doen - alleen de verbindingen tussen punten tellen. Zo kun je het probleem weergeven met grafen: schema’s die tonen welke punten (knooppunten) met elkaar verbonden zijn.

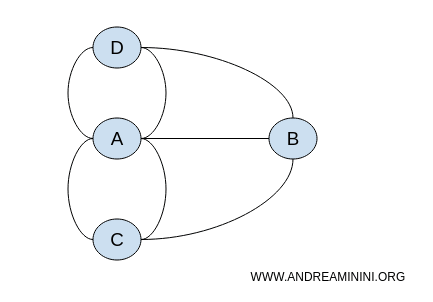
De exacte vorm of positie van de knooppunten maakt niets uit. Zolang de verbindingen gelijk blijven, spreken we van topologische gelijkwaardigheid.

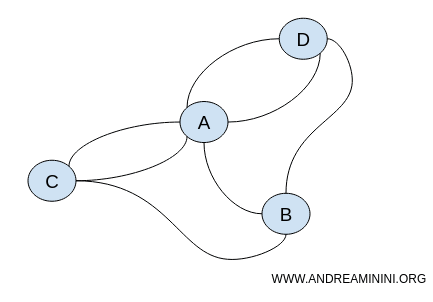
Euler had hiermee iets revolutionairs ontdekt: sommige eigenschappen van een ruimte blijven hetzelfde, ongeacht de afmetingen. Hij noemde dat een "geometrie van positie" - en legde zo de kiem voor de topologie.

In de negentiende eeuw bouwden wiskundigen als Gauss, Möbius, Riemann, Klein en Listing voort op dit idee. Listing was het die in 1847 het woord "topologie" bedacht. Later maakte Henri Poincaré er een volwaardige wiskundige theorie van, de algebraïsche topologie.

Wist je dat? De wetten van Kirchhoff over elektrische netwerken zijn in feite vroege toepassingen van topologische ideeën: ze gaan niet over afstanden, maar over verbindingen.

Topologische ruimten

Een topologische ruimte is de basis van alles. Formeel schrijven we dat als:

$$ (X, T) $$

waarbij X een verzameling punten is en T de verzameling van alle open verzamelingen (de topologie zelf). Zo’n structuur beschrijft wat het betekent dat iets ‘dichtbij’ is of ‘continu’, zonder dat er getallen aan te pas komen.

Voorbeeld: De rechte lijn van de reële getallen \( \mathbb{R} \) is een klassiek voorbeeld. Een deelverzameling is open als ze rond elk punt een klein interval bevat. Dankzij die simpele regel kunnen we abstracte begrippen als continuïteit en limiet beter begrijpen.

Homeomorfismen: vormen die gelijk blijven door vervorming

Een homeomorfisme is een soort ‘elastische spiegeling’ tussen twee ruimten: een continue en omkeerbare vervorming die geen breuken veroorzaakt. Als twee objecten via zo’n transformatie met elkaar verbonden zijn, zijn ze topologisch identiek.

Voorbeeld: Een koffiekop en een donut zijn homeomorf. Beide hebben één gat, en je kunt de ene in de andere vervormen zonder te scheuren of te lijmen. Alleen de vorm verandert, niet de topologische structuur.

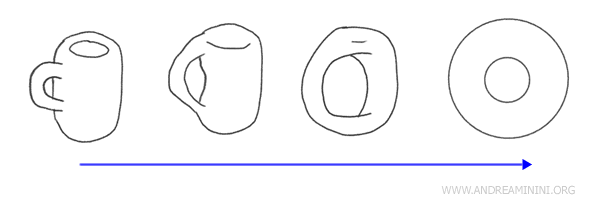
Meetkunde versus topologie

Meetkunde en topologie lijken op elkaar, maar ze kijken naar de wereld op een andere manier.

• Meetkunde houdt zich bezig met maten: afstanden, hoeken en verhoudingen. Een figuur draaien of spiegelen verandert haar niet, zolang de afstanden gelijk blijven.
  

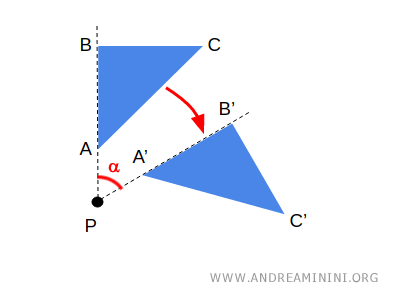
  De klassieke euclidische meetkunde beschrijft onze vertrouwde ruimte, maar in de negentiende eeuw ontdekten wiskundigen dat er ook niet-euclidische meetkunden bestaan, waar de regels anders werken.

• Topologie kijkt niet naar afstanden maar naar verbindingen. Ze onderzoekt hoe vormen continu kunnen worden vervormd zonder dat ze breken. Zo blijft bij het omvormen van een kubus tot een bol de structuur van de ruimte intact.
  

  Voorbeeld: Stel je een kubus van klei voor. Als je hem met je handen zachtjes tot een bol vormt, verandert de vorm, maar niet de onderlinge samenhang van de materie. Dat is een klassiek voorbeeld van een homeomorfisme.
  

Waar de meetkunde zich richt op het meten van vormen, richt de topologie zich op hun identiteit onder vervormingen. Je zou kunnen zeggen: de meetkunde kijkt naar de huid, de topologie naar het skelet.

De vele gezichten van de topologie

Vandaag is de topologie uitgegroeid tot een veelzijdig vakgebied, met toepassingen van pure wiskunde tot kunstmatige intelligentie. Enkele belangrijke deelgebieden zijn:

• Geometrische topologie - bestudeert hoe ruimten zich gedragen bij rekken, buigen en vouwen zonder te scheuren. Hier draait alles om continuïteit en samenhang, niet om afstand.
• Algemene topologie - onderzoekt topologische ruimten op een abstract niveau, met concepten als open en gesloten verzamelingen, compactheid en continuïteit.
• Algebraïsche topologie - gebruikt algebraïsche structuren, zoals groepen, om eigenschappen van ruimten wiskundig vast te leggen.
• Differentiële topologie - verbindt topologie met analyse. Ze onderzoekt ruimten die lokaal op de euclidische ruimte lijken, en maakt het mogelijk om over raakvlakken en gladde krommen te spreken.
• Toegepaste topologie - past topologische technieken toe in echte problemen: van data-analyse en netwerkonderzoek tot biologie en economie.

Topologie is vandaag meer dan een theoretisch spel met vormen. Ze biedt een universele taal om structuur te begrijpen - of het nu gaat om de verbindingen in een netwerk, de vorm van het heelal, of de logica achter complexe data.