Vaste punten in de topologie
In de topologie is een vast punt een waarde die, na toepassing van een functie, onveranderd blijft.
Neem een functie f(x). Een punt p noemen we een vast punt wanneer f(p) = p. Dit betekent dat de functie niets aan de waarde verandert.
$$ f(p) = p $$
Een intuïtief voorbeeld helpt om dit beter te begrijpen. Stel je een object voor dat draait rond een vast middelpunt P.
Door die rotatie veranderen de coördinaten van alle punten van het object, behalve die van het middelpunt zelf.
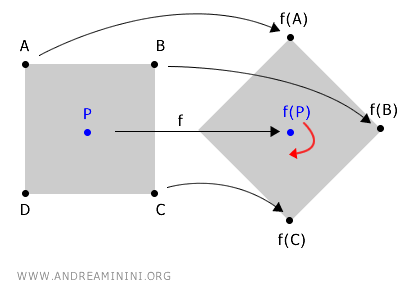
Dat middelpunt P blijft altijd op dezelfde plek. Het is dus een vast punt, want de rotatie verandert er niets aan.
$$ f(P) \longrightarrow P $$
Vaste punten spelen een belangrijke rol in verschillende takken van de wiskunde en duiken ook op in toepassingen zoals numerieke algoritmen, speltheorie en economische modellen.
Een beroemd resultaat waarin vaste punten centraal staan, is het vast-punt-theorema van Brouwer.
Voorbeelden met trigonometrische functies
Laten we kijken naar een concreet voorbeeld met de functie f(x) = sin(x) op het interval [0, 2π].
$$ f(x) = \sin(x) $$
Hier zien we meteen dat p = 0 een vast punt is, want sin(0) = 0.
$$ \sin(0) = 0 $$
Voorbeeld 2
Beschouw nu f(x) = cos(x) op hetzelfde interval.
$$ f(x) = \cos(x) $$
In dit geval is x = 0 géén vast punt, want cos(0) = 1.
Het vaste punt van deze functie bevindt zich echter wél in het interval, ongeveer bij:
$$ \cos(0.73908513) = 0.73908513 $$
De functie en haar invoer komen hier dus bijna precies overeen.
Het vast-punt-theorema van Brouwer
Dit theorema zegt dat:
Elke continue functie die een gesloten n-dimensionale ruimte op zichzelf afbeeldt, ten minste één vast punt heeft.
Het is een bestaanstheorema. Het garandeert dat er minstens één vast punt moet zijn, zonder te vertellen waar het ligt.
Dit principe vormt een belangrijk fundament in de wiskunde en wordt gebruikt om evenwichtspunten aan te tonen, bijvoorbeeld in dynamische systemen en in economische theorie.
Het verhaal van vaste punten gaat nog veel verder, maar dit vormt een goed vertrekpunt om het onderwerp te verkennen.