Het interieur van een deelverzameling
In een topologische ruimte \( X \) noemen we het interieur van een deelverzameling \( A \) de unie van alle open deelverzamelingen die volledig binnen \( A \) liggen. Dit interieur wordt meestal genoteerd als \( \text{Int}(A) \) of \( A^\circ \).
Je kunt het interieur zien als de grootste open verzameling die helemaal in \( A \) past.
Er bestaat dus geen open deelverzameling van \( A \) die groter is dan zijn interieur.
Opmerking: Omdat het interieur een unie is van open deelverzamelingen, is het altijd zelf een open verzameling.
Formeel bestaat het interieur uit alle punten van \( A \) die een open omgeving hebben die volledig binnen \( A \) ligt.
$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ open is in } X \} $$
Een punt \( x \) ligt dus in het interieur zodra er een open verzameling bestaat waarvoor \( x \in U \subseteq A \).
Belangrijk om te onthouden: het interieur van \( A \) hangt af van de topologie op \( X \). Het is dus geen eigenschap van \( A \) zelf, maar van de manier waarop we open verzamelingen in \( X \) definiëren.
Voorbeelden om het idee te verduidelijken
Neem om te beginnen de deelverzameling \( A = [0,1] \) in \( \mathbb{R} \) met de standaardtopologie.
Dit gesloten interval bevat alle getallen tussen 0 en 1, inclusief de grenzen.
Het interieur daarvan is het open interval \( (0,1) \).
$$ \text{Int}(A) = (0,1) $$
De reden is eenvoudig: de punten 0 en 1 hebben geen open omgeving die volledig binnen \( [0,1] \) ligt.
Voorbeeld 2
Beschouw vervolgens \( A = [0,1) \) in dezelfde topologie.
Hoewel dit interval links gesloten en rechts open is, verandert het interieur niet.
\[ \text{Int}(A) = (0,1) \]
Van alle open verzamelingen die binnen \( A \) liggen, is \( (0,1) \) opnieuw de grootste.
Opmerking: In de standaardtopologie op \( \mathbb{R} \) kunnen open verzamelingen alleen bestaan uit unies van open intervallen. Daarom kan 0 niet tot het interieur behoren.
Voorbeeld 3
Nu iets heel anders: neem \( A = [0,1) \) maar plaats het in een ruimte met de discrete topologie.
In zo'n ruimte is elke deelverzameling open.
Daarom heeft elk punt van \( A \) automatisch een open omgeving binnen \( A \).
In de discrete topologie op \( \mathbb{R} \) is werkelijk elke verzameling open: intervallen, eindige sets, willekeurige unies en ook \( [0,1) \) zelf.
Het interieur van \( A \) is in dat geval dus gewoon \( A \):
$$ \text{Int}(A) = A = [0,1) $$
In een discrete topologie valt het interieur altijd samen met de verzameling zelf.
Opmerking: Dit voorbeeld laat goed zien hoe sterk de topologie het begrip interieur bepaalt. De eigenschappen van \( A \) veranderen niet, maar het interieur wel.
Voorbeeld 4
Tot slot, bekijk de ruimte \( X = \{a, b, c\} \), opnieuw met de discrete topologie.
Alle deelverzamelingen zijn hier open, van \( \emptyset \) tot de volledige ruimte.
- De lege verzameling en \( \{a, b, c\} \) zijn open.
- De singletons \( \{a\} \), \( \{b\} \), \( \{c\} \) zijn open.
- Ook de sets met twee elementen zijn open.
Beschouw \( A = \{b, c\} \).
Het interieur is de unie van alle open deelverzamelingen die binnen \( A \) liggen.
In dit geval zijn dat \( \{b\} \), \( \{c\} \) en \( \{b, c\} \) zelf.
\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]
Hier valt het interieur dus opnieuw samen met de originele verzameling.
Opmerking: In een discrete topologie gebeurt dit altijd: voor elke deelverzameling \( S \subseteq X \) geldt dat \( \text{Int}(S) = S \).
Het criterium voor het interieur van een deelverzameling
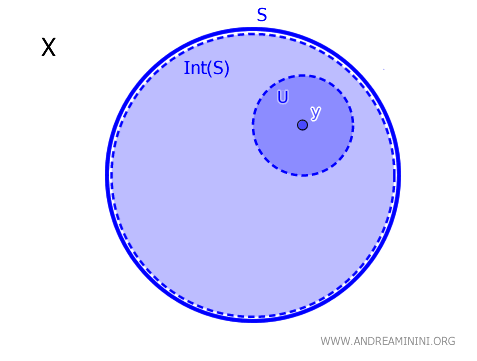
In een topologische ruimte \( X \) zeggen we dat een punt \( y \) tot het interieur van een deelverzameling \( S \) behoort, genoteerd als \( \operatorname{Int}(S) \), wanneer er een open deelverzameling \( U \) bestaat met \( y \in U \subseteq S \). Dit leidt tot het fundamentele criterium: $$ y \in \operatorname{Int}(S) \iff \exists \ U \text{ open, met } y \in U \subseteq S. $$
Een binnenpunt is dus eenvoudig te herkennen: het heeft een open omgeving die volledig binnen \( S \) ligt. Deze formulering is de standaard in de topologie en vormt het uitgangspunt voor tal van andere begrippen.
Het criterium is zowel noodzakelijk als voldoende. Daardoor biedt het een krachtig en praktisch hulpmiddel om te bepalen welke punten tot het interieur van een verzameling behoren.
Bewijs
- Noodzakelijkheid
Als \( y \in \operatorname{Int}(S) \), volgt uit de definitie dat er een open verzameling \( U \) bestaat waarvoor \( y \in U \subseteq S \). Het interieur wordt immers opgebouwd uit alle open deelverzamelingen die in \( S \) zitten. - Voldoende voorwaarde
Bestaat er een open verzameling \( U \) met \( y \in U \subseteq S \), dan is \( y \) per definitie een binnenpunt van \( S \). Het interieur bevat precies alle punten waarvoor zo'n open omgeving bestaat.
Opmerking: Dit criterium maakt helder hoe het begrip binnenpunt volledig steunt op de open verzamelingen van de gekozen topologie. Het vormt de basis voor concepten zoals continuïteit, grenspunten en afsluitingen.
Voorbeeld
Neem het gesloten interval \( A = [1,3] \subseteq \mathbb{R} \) met de standaardtopologie.
$$ A = [1,3] $$
Dit interval bevat alle reële getallen van 1 tot en met 3. Laten we het interieur bepalen.
Het interieur van \( A \)
We zoeken een open verzameling \( U \) die volledig in \( A \) ligt en waarvan alle punten binnenpunten zijn.
- Selectie van \( U \)
Het open interval \( (1,3) \) ligt voor de hand: het is open in \( \mathbb{R} \) en sluit precies aan bij het gesloten interval zonder de randpunten. - Controle van de inclusie
Alle punten van \( (1,3) \) liggen binnen \( [1,3] \). De eindpunten 1 en 3 horen niet bij \( U \), wat overeenkomt met het feit dat zij per definitie geen binnenpunten zijn.
Daarmee is duidelijk dat het interieur van \( A \) gelijk is aan het open interval \( (1,3) \).
Opmerking: De randpunten 1 en 3 liggen niet in het interieur omdat geen enkele open omgeving van deze punten volledig binnen \( A \) valt. Dit maakt zichtbaar hoe het criterium grenspunten onderscheidt van binnenpunten.
Belangrijke eigenschappen van het interieur
Het interieuroperator speelt een centrale rol in de topologie. De onderstaande eigenschappen worden in elk academisch handboek besproken en vormen een solide basis om verder te werken met open verzamelingen en verwante concepten.
- Interieur en unies
De unie van \( \operatorname{Int}(A) \) en \( \operatorname{Int}(B) \) ligt altijd binnen het interieur van \( A \cup B \). Vaak is deze inclusie strikt. $$ \operatorname{Int}(A) \cup \operatorname{Int}(B) \subseteq \operatorname{Int}(A \cup B). $$ - Interieur en doorsneden
Voor doorsneden geldt juist een perfecte overeenkomst: $$ \operatorname{Int}(A) \cap \operatorname{Int}(B) = \operatorname{Int}(A \cap B). $$ - Interieur van het complement
Een klassieke relatie verbindt het interieur van het complement met de afsluiting van \( A \): $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A). $$ - Afsluiting van het complement
In dezelfde geest geldt: $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A). $$
Verdere opmerkingen
Enkele aanvullende inzichten die helpen om het interieur in de juiste context te plaatsen:
- Open verzamelingen binnen een verzameling
Als \( U \) open is en \( U \subseteq A \), dan ligt \( U \) automatisch in \( \operatorname{Int}(A) \). Het interieur is immers de grootste open deelverzameling van \( A \). - De inclusie-eigenschap van het inwendige
Voor alle verzamelingen \( A \subseteq B \) geldt: $$ \operatorname{Int}(A) \subseteq \operatorname{Int}(B). $$ - Karakterisatie van open verzamelingen
Een verzameling is open precies wanneer zij samenvalt met haar interieur: $$ A = \operatorname{Int}(A). $$ - Het interieur bepalen met R
Dankzij de uitgebreide analyse- en visualisatiemogelijkheden van R kan men het interieur van een verzameling efficiënt onderzoeken, ook in complexe situaties.
Deze eigenschappen vormen samen een helder en samenhangend beeld van hoe het interieur zich gedraagt binnen een topologische ruimte en hoe het samenwerkt met andere fundamentele topologische bewerkingen.