De standaardtopologie op een verzameling
De standaardtopologie op \( \mathbb{R} \) wordt opgebouwd uit open intervallen \( (a, b) \) met \( a < b \). Elke eindige of oneindige vereniging van zulke intervallen vormt een open verzameling in deze topologie.
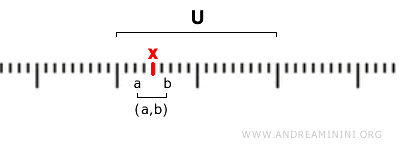
Formeel heet een deelverzameling \( U \subseteq \mathbb{R} \) open als voor elk punt \( x \in U \) een open interval \( (a, b) \) bestaat waarvoor \( x \in (a, b) \) en \( (a, b) \subseteq U \).
$$ x \in (a,b) \subseteq U $$
Met andere woorden: elk punt van een open verzameling ligt binnen een open interval dat volledig in die verzameling is opgenomen.
In de standaardtopologie beschouwen we de volgende soorten verzamelingen als open:
- Open intervallen
De open verzamelingen op \( \mathbb{R} \) zijn precies de open intervallen \( (a, b) \) met \( a < b \), en elke mogelijke vereniging van zulke intervallen, of die nu eindig of oneindig is. - Operaties met open verzamelingen
De eigenschappen van open verzamelingen blijven behouden bij bepaalde bewerkingen:
- Vereniging: Een willekeurige vereniging van open verzamelingen is opnieuw open.
- Eindige doorsnede: De doorsnede van een eindig aantal open verzamelingen blijft open.
De standaardtopologie is slechts één voorbeeld van de vele mogelijke topologieën op een verzameling \( X \). Ze heet “standaard” omdat ze de meest gebruikte is en een centrale rol speelt in veel takken van de wiskunde.
Deze topologie is bijzonder omdat ze intuïtieve begrippen als nabijheid, openheid en continuïteit op een formele manier beschrijft, vooral op de reële rechte \( \mathbb{R} \).
Opmerking: Op \( \mathbb{R} \) en in andere ruimten bestaan ook alternatieve topologieën, gebaseerd op andere bases. Zulke topologieën worden gebruikt om specifieke eigenschappen te onderzoeken of om wiskundige structuren vanuit een ander perspectief te bekijken.
Voorbeeld: de basis van de standaardtopologie
De basis van de standaardtopologie op \( \mathbb{R} \) bestaat uit alle open intervallen \( (a, b) \) met \( a < b \).
$$ B = \{ (a,b) \subset \mathbb{R} \ | \ a<b \} $$
Een belangrijk kenmerk van deze topologie is dat voor elk punt \( x \) in een open verzameling \( U \) een open interval bestaat met middelpunt \( x \) dat volledig in \( U \) ligt. Dit sluit precies aan bij de definitie van openheid binnen de standaardtopologie.
$$ \forall \ x \in U \ \exists \ \epsilon>0 \ | \ (x-\epsilon, x+\epsilon) \subseteq U $$
Zo wordt \( U \) erkend als open in de standaardtopologie op \( \mathbb{R} \). Deze topologie is de natuurlijke keuze op de reële rechte, vooral om begrippen als continuïteit en limiet wiskundig te formuleren.
Voorbeeld 2: het interval (0,1)
Beschouw het interval \( (0,1) \), waarin de eindpunten \( 0 \) en \( 1 \) niet zijn opgenomen. We onderzoeken of dit interval een topologische ruimte vormt onder de standaardtopologie.
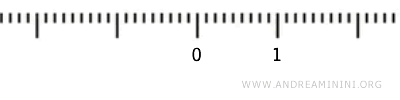
In de geïnduceerde topologie is een deelverzameling \( U \subset (0, 1) \) open als, voor elk punt \( x \in U \), er een open interval \( (a, b) \) in \( \mathbb{R} \) bestaat waarvoor \( x \in (a, b) \) en \( (a, b) \cap (0,1) \subseteq U \).
Het interval \( (0,1) \) kan worden beschreven als de doorsnede van verschillende open verzamelingen in de standaardtopologie van \( \mathbb{R} \). Daardoor erft het een goed gedefinieerde topologische structuur.
Het interval \( (0,1) \) vormt dus een topologische ruimte met de topologie die wordt geïnduceerd door de standaardtopologie op \( \mathbb{R} \).
Bijvoorbeeld: de verzamelingen \( (0.1, 0.5) \), \( (0.2, 0.9) \) of hun vereniging \( (0.1, 0.5) \cup (0.6, 0.8) \) zijn open in \( (0,1) \) volgens de geïnduceerde topologie. Met andere woorden, de open verzamelingen van \( (0,1) \) zijn precies die open verzamelingen van \( \mathbb{R} \) waarvan de doorsnede met \( (0,1) \) geheel binnen dit interval ligt.
Aangezien \( (0,1) \) een topologische deelruimte van \( \mathbb{R} \) is, deelt het alle fundamentele eigenschappen van de reële rechte.
Voorbeeld 3: een eindige verzameling
Neem nu de eindige verzameling \( X = \{1,2,3\} \), bestaande uit drie natuurlijke getallen. Kan \( X \) worden uitgerust met een topologische structuur die is afgeleid van de standaardtopologie op \( \mathbb{R} \)?
In dit geval kunnen de afzonderlijke elementen van \( X \) niet als open worden beschouwd, omdat de basis van de standaardtopologie uit open intervallen bestaat. Dat past niet bij een discrete verzameling als \( X \).
Beschouw bijvoorbeeld het element \( \{2\} \) in \( X \). Dit ligt wel binnen een open interval \( (2-\epsilon, 2+\epsilon) \), maar dat interval bevat oneindig veel reële getallen die niet tot \( X \) behoren. Daarom is \( \{2\} \) geen open verzameling in de standaardtopologie op \( \mathbb{R} \).
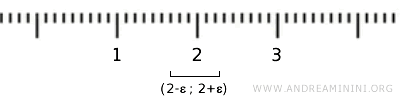
Als we \( X \) beschouwen als deelverzameling van \( \mathbb{R} \), dan bevat de “geïnduceerde topologie” of “deelruimtetopologie” op \( X \) slechts twee open verzamelingen: de lege verzameling en \( X \) zelf. Topologisch gezien is dit een triviaal geval.
Om een eindige verzameling zoals \( X \) van een rijkere structuur te voorzien, gebruikt men meestal de discrete topologie, waarin alle deelverzamelingen van \( X \) per definitie open zijn.