Topologische transformaties

Topologische transformaties zijn manieren om een ruimte te vervormen zonder haar essentiële structuur te veranderen. Je kunt eraan trekken, duwen of buigen - zolang je niets scheurt of aan elkaar plakt, blijft de topologie hetzelfde.

Topologie is de wiskunde van vormen en ruimten die hun identiteit behouden, hoezeer ze ook worden uitgerekt of vervormd. Ze kijkt niet naar afstanden of hoeken, maar naar wat er echt onveranderlijk blijft: verbondenheid, gaten en continuïteit.

Hier zijn enkele basisprincipes van topologische transformaties:

• Continuïteit
  Een topologische transformatie verloopt zonder sprongen of breuken. Kleine veranderingen aan het begin leiden tot kleine veranderingen aan het eind.
• Verbondenheid en nabijheid
  Punten die in het origineel met elkaar verbonden zijn of dicht bij elkaar liggen, blijven dat ook na de transformatie.
• Zonder scheuren of plakken
  Je mag vormen vervormen, maar niet breken of samenvoegen. Een donut kun je dus omvormen tot een koffiekopje - beide hebben immers één gat. Maar een bol kan geen donut worden zonder te scheuren.

Waarvoor dient dit? Topologische transformaties duiken op in allerlei vakgebieden: van zuivere wiskunde en knooptheorie tot natuurkunde, informatica en zelfs robotica. Ze helpen ons begrijpen welke eigenschappen van vormen en structuren fundamenteel zijn en welke niet.

Soorten topologische transformaties

Er bestaan verschillende soorten transformaties, elk met hun eigen manier om continuïteit te behouden.

• Homeomorfismen
  Dit zijn transformaties die omkeerbaar en continu zijn. Je kunt de ruimte heen en weer vervormen zonder iets te breken. De beroemde vergelijking: een donut en een koffiekopje zijn homeomorf - topologisch gezien identiek.
• Isotopieën
  Een isotopie is een vloeiende reeks homeomorfismen, waarbij elke stap zelf ook continu is. Denk aan het langzaam verschuiven van een knoop langs een touw, zonder het touw aan te spannen of los te laten.
• Homotopieën
  Homotopieën beschrijven hoe één functie geleidelijk in een andere verandert zonder topologische breuken. Het uitrekken en weer loslaten van een veer is een intuïtief voorbeeld: elke tussenfase is een homotopie.
• Diffomorfismen
  Deze zijn net iets verfijnder: ze zijn niet alleen continu, maar ook glad en afleidbaar. Ze spelen een rol in de differentieële topologie, waar oppervlakken niet alleen verbonden maar ook glad moeten blijven.

Deze categorieën tonen hoe ruimten zich kunnen vervormen zonder hun identiteit te verliezen - elk met een ander niveau van wiskundige strengheid.

Geometrische vs. topologische transformaties

Topologische transformaties verschillen van geometrische doordat ze zich niet bekommeren om afstanden of hoeken. In de geometrie blijft alles meetbaar gelijk; in de topologie tellen alleen de verbindingen en gaten.

• Geometrische transformaties
  Hierbij blijven afstanden, hoeken en vormen behouden. Denk aan translaties, rotaties of spiegelingen.

  Een rotatie verandert bijvoorbeeld de oriëntatie, maar niet de afstand tussen punten.

• Topologische transformaties
  Hierbij mogen afstanden en hoeken veranderen, zolang de structuur behouden blijft. Een cirkel kan worden uitgerekt tot een ovaal, of een donut tot een koffiekopje - zonder dat er iets breekt.

  In topologische termen: beide hebben één gat, en dat is wat telt.

Geometrie draait dus om meten en vormen, terwijl topologie draait om structuur en verbinding. Wat onveranderd blijft onder alle zachte vervormingen, dát is wat de topologie bestudeert.

Kunnen transformaties zowel geometrisch als topologisch zijn?

Ja! Sommige transformaties zijn beide: ze zijn continu én behouden afstanden of hoeken. Zulke transformaties zijn zowel topologisch als geometrisch geldig.

• Isometrieën
  Translaties, rotaties en spiegelingen zijn hier voorbeelden van. Ze veranderen de positie, maar niet de afstanden of vormen. Ze zijn dus tegelijk geometrische en topologische transformaties.
  
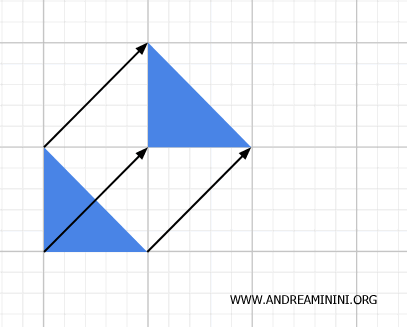
• Similariteiten
  Dit zijn schaalvergrotingen of verkleiningen die de vorm behouden, inclusief hoeken en verhoudingen. Ze zijn geometrisch omdat ze met afmetingen te maken hebben, maar ook topologisch omdat de structuur hetzelfde blijft.

Geometrie en topologie staan dus niet lijnrecht tegenover elkaar. Soms lopen ze naadloos in elkaar over - en precies daar wordt de wiskunde pas echt interessant.