Reguliere ruimten in de topologische theorie

Reguliere ruimten hebben een sterkere scheidingseigenschap dan Hausdorff-ruimten. In de taal van de scheidingsaxioma's behoren zij tot de \( T_3 \)-ruimten: \( T_1 \)-ruimten waarin punten en gesloten verzamelingen op een gecontroleerde manier uit elkaar kunnen worden gehouden.

Een interessante bijkomstigheid is dat een reguliere ruimte met een aftelbare basis metriseerbaar is. Volgens de stelling van Urysohn kan haar topologie dan worden opgevat als afkomstig van een passende metriek. Dat maakt dergelijke ruimten bijzonder goed hanteerbaar.

Het verschil met Hausdorff-ruimten

Een Hausdorff-ruimte garandeert dat twee verschillende punten elk een eigen open buurt hebben die elkaar niet overlappen. In een reguliere ruimte gaat men een stap verder: ook een punt en een gesloten verzameling die dat punt niet bevat, moeten van elkaar te scheiden zijn door twee open verzamelingen. Dat maakt de structuur van reguliere ruimten fijner en preciezer.

Opmerking. Niet elke reguliere ruimte is normaal. Normale ruimten (de \( T_4 \)-ruimten) stellen een strengere eis: elk paar disjuncte gesloten verzamelingen moet door disjuncte open verzamelingen zijn te scheiden. Elke normale ruimte is dus regulier, maar het omgekeerde geldt niet algemeen.  

Regelmatigheid is daarmee één van de vele bouwstenen van de scheidingsaxioma's. Er bestaan Hausdorff-ruimten die niet regulier zijn en reguliere ruimten die niet Hausdorff zijn. De hiërarchie van deze axioma's vormt een nuttig instrument om de manier waarop een ruimte haar elementen onderscheidt beter te begrijpen.

Een concreet voorbeeld

Een klassiek en intuïtief voorbeeld van een reguliere ruimte is de reële rechte \( \mathbb{R} \), uitgerust met de standaardtopologie. Dit voorbeeld laat precies zien hoe de scheidingseigenschap werkt.

Neem een punt \( x = 2 \) en de gesloten verzameling \[ C = (-\infty, 0] \cup [5, \infty). \] Het punt behoort duidelijk niet tot \( C \), en de verzameling is gesloten zoals men mag verwachten.

We willen nu open verzamelingen vinden die het punt en de gesloten verzameling gescheiden houden. Het complement van \( C \) is open en bevat intervallen waarin \( x \) ligt. Een natuurlijke keuze is het interval \( (0, 5) \).

Om twee open verzamelingen te construeren, kiezen we getallen \( c \) en \( d \) waarvoor \[ 0 < c < 2 < d < 5. \] Met \( c = 1 \) en \( d = 3 \) hebben we een eenvoudige en praktische keuze.

Daarmee definiëren we:

• \( U = (1, 3) \), een open buurt van het punt \( x = 2 \).
• \( V = (-\infty, 1) \cup (3, \infty) \), dat de volledige gesloten verzameling \( C \) omvat.

Deze twee verzamelingen overlappen niet en vervullen precies wat de definitie van regelmatigheid vereist.

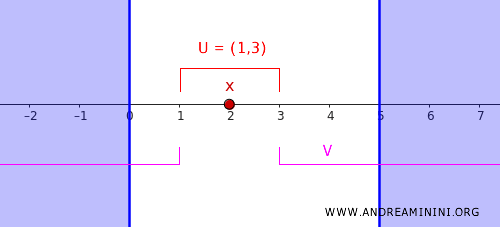
Het voorbeeld toont helder hoe een punt en een gesloten verzameling in \( \mathbb{R} \) door open verzamelingen kunnen worden gescheiden. Dit bevestigt dat de reële rechte met haar standaardtopologie een reguliere ruimte is.

Notities

Wie zich verder wil verdiepen in regelmatigheid, vindt houvast in de scheidingsaxioma's:

• De scheidingsaxioma's
  Deze axioma's vormen een gestructureerde manier om te begrijpen hoe fijnmazig een ruimte is opgebouwd. Eigenschappen als Hausdorff, regulier en normaal geven elk op hun eigen niveau aan hoe goed een ruimte haar punten en verzamelingen kan onderscheiden.

  Opmerking. Een ruimte is Hausdorff wanneer ieder paar verschillende punten beschikt over disjuncte open buurten. Een ruimte is regulier wanneer dit principe ook geldt voor een punt en een gesloten verzameling die dat punt niet bevat. Deze eigenschappen geven een indruk van de "resolutie" van een topologie: hoe hoger, hoe scherper de structuur van de ruimte zichtbaar wordt.

Enzovoort.