Hausdorff-ruimten

Een Hausdorff-ruimte is een topologische ruimte waarin elk tweetal verschillende punten van elkaar kan worden gescheiden door twee open verzamelingen die elkaar nergens overlappen. Dat betekent dat ieder punt zijn eigen open omgeving heeft waarmee het duidelijk te onderscheiden is van de rest.

Concreet houdt dit in dat voor elk paar $ x \ne y $ open verzamelingen $ U $ en $ V $ bestaan met $ x \in U $, $ y \in V $ en $ U \cap V = \emptyset $. Twee punten kunnen dus altijd netjes uit elkaar worden gehouden.

Deze scheidingseigenschap sluit goed aan bij ons vertrouwde beeld uit de Euclidische meetkunde, waar punten altijd van elkaar te isoleren zijn door geschikte omgevingen. In de analyse en de topologie is dit bijzonder belangrijk, omdat Hausdorff-ruimten een solide basis bieden voor het begrip convergentie en de zekerheid dat limieten uniek zijn.

Een bekend resultaat is dat in iedere Hausdorff-ruimte enkelvoudige punten gesloten verzamelingen zijn. Het complement van één punt is namelijk altijd open, waardoor het punt zelf automatisch gesloten is.

Voorbeelden
Waarom de Hausdorff-eigenschap belangrijk is

Voorbeelden

Voorbeeld 1

Neem de standaardtopologie op de reële rechte $\mathbb{R}$, gebaseerd op open intervallen.

visualisatie van de reële lijn

In deze topologie is een singleton $ \{x\} $ geen open verzameling. Dat komt omdat een open verzameling rond elk punt een interval moet bevatten en een enkel punt zo’n interval niet kan leveren.

Uitleg: Een singleton heeft geen ruimte om een open interval te bevatten. Daarom kan $ \{x\} $ niet open zijn.

Het complement $ \mathbb{R} \setminus \{x\} $ is daarentegen wél open.

open omgeving van het complement van een punt

Hieruit volgt dat $ \{x\} $ gesloten is.

Bovendien is $\mathbb{R}$ met de standaardtopologie een Hausdorff-ruimte. Voor elk tweetal verschillende punten kun je immers twee open intervallen vinden die ruim genoeg zijn om elkaar niet te overlappen.

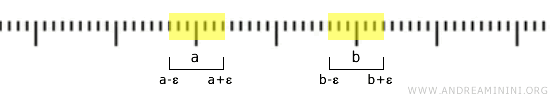
open intervallen rond a en b

Als $ a < b $, kies dan een $ \varepsilon > 0 $ zodat $ a + \varepsilon < b - \varepsilon $. De intervallen $ (a - \varepsilon, a + \varepsilon) $ en $ (b - \varepsilon, b + \varepsilon) $ liggen dan volledig uit elkaar.

Dit laat zien hoe natuurlijk de Hausdorff-eigenschap in $\mathbb{R}$ voorkomt.

Voorbeeld 2

Beschouw nu de eindige ruimte $ X = \{1, 2, 3\} $ met de discrete topologie.

Hier is elke deelverzameling open. Singletons, paren en de hele ruimte zelf: alles is open.

de lege verzameling $ \emptyset $
de singletons $ \{1\}, \{2\}, \{3\} $
de paren $ \{1, 2\}, \{1, 3\}, \{2, 3\} $
de volledige verzameling $ \{1, 2, 3\} $

In totaal zijn er $ 2^3 = 8 $ open verzamelingen, precies alle mogelijke subsets.

Omdat elke singleton open is, kun je elke twee verschillende punten meteen scheiden door respectievelijk $ \{x\} $ en $ \{y\} $. Dit maakt $ X $ automatisch een Hausdorff-ruimte.

Bijvoorbeeld:

$$ \{1\} \cap \{2\} = \emptyset $$

Zijn singletons in de discrete topologie open of gesloten?

Het verrassende antwoord is: beide. In de topologie kunnen verzamelingen namelijk tegelijkertijd open en gesloten zijn. Zulke verzamelingen worden clopen genoemd.

In de discrete topologie is elk singleton open. Zijn complement is eveneens open, omdat ook het complement een deelverzameling is van $ X $. Daardoor is elk singleton automatisch gesloten.

Voor $ X = \{1, 2, 3\} $ is $ \{1\} $ open. Het complement $ \{2, 3\} $ is ook open. Daarom is $ \{1\} $ zowel open als gesloten.

In de discrete topologie zijn alle singletons dus clopen.

Het grote verschil met de standaardtopologie is dat daar niet elke deelverzameling open is. In de standaardtopologie moeten verzamelingen voldoen aan bepaalde structurele voorwaarden om open te zijn. In de discrete topologie is alles open, zonder uitzondering.

Waarom de Hausdorff-eigenschap belangrijk is

De Hausdorff-eigenschap heeft een paar zeer nuttige gevolgen. Een van de belangrijkste is dat een convergente rij in een Hausdorff-ruimte slechts één limiet kan hebben. Dit maakt de theorie van limieten betrouwbaar en voorspelbaar.

Uniciteit van de limiet
Een rij kan in een Hausdorff-ruimte nooit naar twee verschillende punten convergeren. Als dat wel zo was, zouden die twee limieten door disjuncte open omgevingen gescheiden kunnen worden en zouden de termen van de rij zich uiteindelijk in beide omgevingen tegelijk moeten bevinden, wat onmogelijk is.

Bewijs: Laat $ X $ een Hausdorff-ruimte zijn. Neem een rij $ x_1, x_2, x_3, \dots $ die zowel naar $ x $ als naar $ y $ convergeert, met $ x \ne y $. Voor elke open omgeving $ U $ van $ x $ bestaat een index $ N $ zodat $ x_n \in U $ zodra $ n > N $. Voor elke open omgeving $ V $ van $ y $ bestaat een $ M $ zodat $ x_n \in V $ zodra $ n > M $.

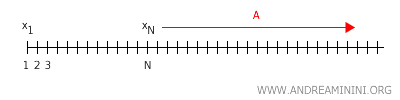
schematische rij die naar x convergeert

Omdat $ x \ne y $, bestaan er disjuncte open omgevingen $ U $ en $ V $. De rij zou zich voor grote $ n $ dus in beide moeten bevinden, wat onmogelijk is. Daarom kan de limiet niet dubbel zijn.

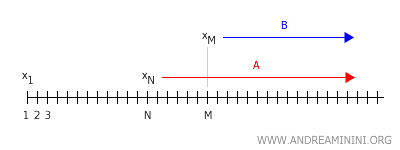
alternatieve vermeende limiet y

De conclusie is duidelijk: in een Hausdorff-ruimte is de limiet van een rij altijd uniek.