Afsluiting van een verzameling

De afsluiting van een verzameling $ A $ in een topologische ruimte $ X $ is het snijpunt van alle gesloten verzamelingen die $ A $ bevatten. Deze afsluiting wordt genoteerd als $ \text{Cl}(A) $.

Intuïtief kun je de afsluiting zien als de kleinste gesloten verzameling waarin alle punten van $ A $ zijn ondergebracht.

Er bestaat dus geen gesloten verzameling die $ A $ bevat en toch strikt kleiner is dan zijn afsluiting.

Opmerking : Deze eigenschap volgt direct uit de definitie. Omdat de afsluiting wordt gevormd als het snijpunt van alle gesloten verzamelingen die $ A $ bevatten, is zij per definitie de minimale gesloten verzameling met die eigenschap. Met andere woorden, de afsluiting bestaat precies uit de elementen die alle deze gesloten verzamelingen gemeenschappelijk hebben.

Formeel kan men de afsluiting van $ A $ als volgt noteren:

$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ en } C \text{ gesloten is in } X \} $$

Hier geeft $ \text{Cl}(A) $ de afsluiting van $ A $ aan, terwijl het symbool $ \bigcap $ staat voor het snijpunt van alle gesloten verzamelingen $ C $ die $ A $ bevatten.

De afsluiting van $ A $ omvat niet alleen de punten van $ A $ zelf, maar ook alle ophopingspunten van $ A $ in de ruimte $ X $.

Opmerking : Het is belangrijk te beseffen dat de afsluiting van een verzameling $ A $ in hoofdzaak wordt bepaald door de topologie van de ruimte $ X $, en veel minder door de intrinsieke eigenschappen van $ A $. Dezelfde verzameling kan dus, afhankelijk van de gekozen topologie, verschillende afsluitingen hebben.

Een illustratief voorbeeld
Het sluitingstheorema van een verzameling
Eigenschappen van de afsluiting in topologische ruimten
Essentiële observaties

Een illustratief voorbeeld

Neem de verzameling $ A = (0, 1) $ in $ \mathbb{R} $, voorzien van de gebruikelijke topologie.

Dit is het open interval dat alle reële getallen strikt tussen 0 en 1 bevat, zonder de eindpunten.

In deze situatie is de afsluiting van $ A $ gelijk aan het gesloten interval $ [0,1] $.

$$ \text{Cl}(A) = [0,1] $$

Deze verzameling bevat het oorspronkelijke interval $ (0,1) $ én de bijbehorende ophopingspunten, namelijk 0 en 1.

Opmerking : In de gebruikelijke topologie op $ \mathbb{R} $ heet een verzameling gesloten wanneer zij al haar ophopingspunten bevat. Een punt is een ophopingspunt als elke omgeving ervan minstens één ander punt van de verzameling bevat. Zo is bijvoorbeeld het snijpunt van de gesloten intervallen [0,2] en [-1,1] gelijk aan [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$ Er bestaat geen kleiner gesloten interval dat $ (0,1) $ bevat.

Voorbeeld 2/nl/math/de-monotoniciteit-van-de-afsluiting

Beschouwen we nu de verzameling $ A = [0, 1) $ in $ \mathbb{R} $, opnieuw met de gebruikelijke topologie.

Dit interval is links geslo/nl/math/de-monotoniciteit-van-de-afsluitingten en rechts open, en bevat alle reële getallen van 0 inbegrepen tot 1 uitgesloten.

Ook hier blijkt de afsluiti/nl/math/de-monotoniciteit-van-de-afsluitingng gelijk te zijn aan $ [0,1] $.

$$ \text{Cl}(A) = [0,1] $$

Het punt 0 behoort al tot $ A $, terwijl 1 een ophopingspunt is dat net buiten $ A $ ligt.

Daarom wordt ook het rechter eindpunt toegevoegd, en ontstaat opnieuw het gesloten interval $ [0,1] $, de kleinst mogelijke gesloten verzameling die $ A $ bevat.

Opmerking : Dit voorbeeld maakt duidelijk hoe de definitie van afsluiting automatisch alle ophopingspunten omvat. Opnieuw geldt bijvoorbeeld dat $$ [0,2] \cap [-1,1]=[0,1] $$

Voorbeeld 3

We bekijken opnieuw dezelfde verzameling $ A = [0,1) $, maar nu in een ruimte $ X $ met de discrete topologie.

In een discrete topologie is elke deelverzameling tegelijkertijd open en gesloten.

Open verzameling
Elke deelverzameling van $ X $ is open. Omdat $ A \subset X $, is $ A $ dus een open verzameling.
Gesloten verzameling
Elke deelverzameling is ook gesloten, aangezien het complement ervan open is. Het complement $ X/A $ is dus open, en daarmee is $ A $ gesloten.

Men zegt dat elke verzameling in dit geval clopen is, dat wil zeggen tegelijk open en gesloten.

Daarom valt de afsluiting van $ A $ hier exact samen met $ A $ zelf.

$$ \text{Cl}(A) = [0,1) $$

/fr/math/fermeture-du-complement-et-complement-de-lainterieur-daun-ensembleDe kleinste gesloten verzameling die $ A $ bevat, is dus eenvoudigweg $ A $ zelf.

Opmerking : Dit voorbeeld laat goed zien hoe sterk de keuze van de topologie het begrip afsluiting beïnvloedt. Of een verzameling gesloten is, hangt af van de topologische structuur van $ X $, niet van de verzameling op zichzelf.

Voorbeeld 4

Beschouw tot slot een topologische ruimte $ X $ die bestaat uit de punten $ \{a, b, c\} $, opnieuw met de discrete topologie.

In deze ruimte is elke deelverzameling open:

$ \emptyset $ en $ \{a, b, c\} $ zijn per definitie open.
De singletons $ \{a\} $, $ \{b\} $ en $ \{c\} $ zijn eveneens open.
Ook combinaties zoals $ \{a, b\} $, $ \{a, c\} $ en $ \{b, c\} $ zijn open verzamelingen.

Aangezien het complement van elke deelverzameling opnieuw open is, zijn alle deelverzamelingen tegelijk open en gesloten.

Nemen we $ A = \{b, c\} $, dan is deze verzameling zowel open als gesloten.

De afsluiting van $ A $, genoteerd als $ \text{Cl}(A) $, is het snijpunt van alle gesloten verzamelingen die $ A $ bevatten. In dit geval verandert er niets.

We krijgen dus:

\[ \text{Cl}(A) = \{b, c\} \]

In een discrete topologie is elke verzameling al gesloten, waardoor de afsluiting altijd samenvalt met de oorspronkelijke verzameling.

Opmerking : Dit is eenvoudig te controleren. De gesloten verzamelingen die $ A $ bevatten zijn $ \{b, c\} $ en $ \{a, b, c\} $. $$ \text{Cl}(A) = \{b, c\} \cap \{a, b, c\} = \{b, c\} $$ Het snijpunt is precies $ A $, en dus geldt $ \text{Cl}(A) = A $.

Het sluitingstheorema van een verzameling

In een topologische ruimte $ X $ behoort een punt $ y $ tot de afsluiting van een deelverzameling $ S $, genoteerd als $ \text{Cl}(S) $, dan en slechts dan wanneer elke open verzameling $ U $ die $ y $ bevat, een niet-lege doorsnede heeft met $ S $: $ y \in \text{Cl}(S) \iff \forall \ U \text{ open met } y \in U,\ U \cap S \neq \emptyset $.

Intuïtief betekent dit dat een punt tot de afsluiting van $ S $ behoort zodra je het niet kunt "isoleren" van $ S $ met behulp van open verzamelingen. Elke open buurt rond dat punt raakt $ S $ onvermijdelijk.

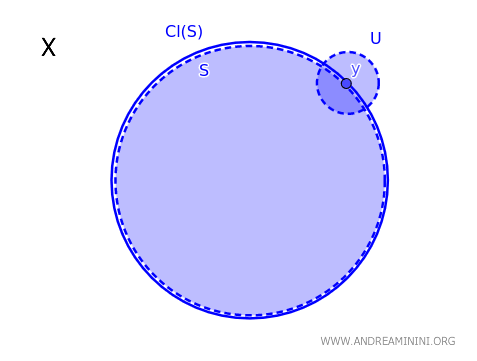
grafische voorstelling van het criterium voor de afsluiting van een verzameling

Dit theorema biedt een bijzonder bruikbaar criterium om na te gaan of een punt tot de afsluiting van een verzameling behoort, zonder expliciet alle gesloten verzamelingen te hoeven beschouwen.

Bewijs

Noodzakelijke voorwaarde : Stel dat $ y \in \text{Cl}(S) $. Volgens de definitie van afsluiting kan geen enkele open verzameling die $ y $ bevat, disjunct zijn van $ S $. Elke open buurt van $ y $ moet dus minstens één punt van $ S $ bevatten. Dit komt overeen met het feit dat de afsluiting zowel de inwendige punten als de ophopingspunten van $ S $ omvat. Een ophopingspunt is een punt waarvoor elke buurt een punt van $ S $ bevat, al dan niet verschillend van het punt zelf.
Voldoende voorwaarde : Omgekeerd, als elke open verzameling die $ y $ bevat, $ S $ snijdt, dan kan $ y $ niet buiten de afsluiting van $ S $ liggen. Het punt $ y $ is dan ofwel een element van $ S $, ofwel een ophopingspunt van $ S $. In beide gevallen geldt dat $ y \in \text{Cl}(S) $.

Opmerking : Dit theorema is een hoeksteen van de algemene topologie. Het maakt de abstracte definitie van afsluiting concreet door haar te verbinden met het gedrag van open verzamelingen. Het wordt frequent gebruikt bij de studie van continuïteit, convergentie van rijen en netten, en in vele fundamentele redeneringen.

Voorbeeld

Beschouw de verzameling $ A = (0, 2) $ in $ \mathbb{R} $, uitgerust met de gebruikelijke topologie. Dit is een open interval van de reële getallen.

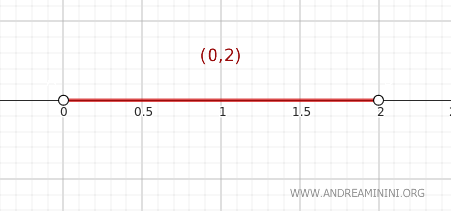
open interval op de reële getallenlijn met zijn afsluiting

We gebruiken het theorema om te bepalen of een gegeven punt $ y $ tot $ \text{Cl}(A) $ behoort.

Kies bijvoorbeeld het punt $ y = 2 $.

Volgens het sluitingstheorema behoort $ y $ tot $ \text{Cl}(A) $ precies dan wanneer elke open verzameling die $ y $ bevat, een doorsnede heeft met $ A $.

Analyse van de buurten van $ y $ : Elk open interval dat $ y = 2 $ bevat, zoals $ (1{,}9, 2{,}1) $, $ (1{,}95, 2{,}05) $ of $ (1{,}99, 2{,}01) $, bevat noodzakelijk punten van $ A = (0, 2) $, bijvoorbeeld $ 1{,}95 $ of $ 1{,}99 $.
Conclusie : Omdat geen enkele open buurt van $ y $ disjunct is van $ A $, volgt uit het theorema dat $ y = 2 $ inderdaad tot $ \text{Cl}(A) $ behoort.

Het punt $ y = 2 $ is dus een aanhechtingspunt van $ A $.

$$ y \in \text{Cl}(A) $$

Daaruit volgt dat de afsluiting van $ A $ het gesloten interval $ \text{Cl}(A) = [0, 2] $ is, waarin ook het punt $ 2 $ is opgenomen.

Eigenschappen van de afsluiting in topologische ruimten

Hieronder bespreken we enkele fundamentele eigenschappen van de afsluiting, samen met hun relatie tot andere topologische begrippen zoals het inwendige en het complement.

Inwendige van het complement en complement van de afsluiting
Het inwendige van het complement van een verzameling $ A $ is gelijk aan het complement van haar afsluiting: $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$
Afsluiting van het complement en complement van het inwendige
De afsluiting van het complement van $ A $ valt samen met het complement van het inwendige van $ A $: $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$

Essentiële observaties

Tot slot volgen enkele kernachtige eigenschappen van de afsluiting, die in vrijwel elke topologische context terugkeren:

Als $ C $ gesloten is en $ A \subseteq C $, dan geldt $ \text{Cl}(A) \subseteq C $
De afsluiting van $ A $ is de kleinste gesloten verzameling die $ A $ bevat en ligt daarom in elk gesloten superset van $ A $.
Monotonie van de afsluiting
Uit $ A \subseteq B $ volgt steeds $ \text{Cl}(A) \subseteq \text{Cl}(B) $.
Karakterisatie van gesloten verzamelingen
Een verzameling $ A $ is gesloten dan en slechts dan wanneer zij samenvalt met haar afsluiting: $$ A = \text{Cl}(A) $$
Afsluiting als unie
Indien $ A' $ de verzameling van ophopingspunten van $ A $ is, dan geldt: $$ \text{Cl}(A) = A \cup A' $$
Idempotentie
Het herhaald toepassen van de afsluitingsoperator verandert niets aan het resultaat: $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$
Insluiting
Elke verzameling is altijd een deelverzameling van haar eigen afsluiting: $$ A \subseteq \text{Cl}(A) $$

Verdere verdieping en aanvullende voorbeelden volgen in volgende secties.