De discrete topologie uitgelegd
De discrete topologie \( T \) is de meest verfijnde topologie die men op een verzameling \( X \) kan definiëren. Ze omvat namelijk alle mogelijke deelverzamelingen van \( X \).
Dat betekent dat elke deelverzameling van \( X \) automatisch een open verzameling is. In de discrete topologie is dus niets uitgesloten: alles wat men zich kan voorstellen als subset van \( X \), wordt beschouwd als open.
Elk element van \( X \) vormt op zichzelf een open verzameling. Anders gezegd: elk punt staat volledig op zichzelf en is geïsoleerd van de andere. Er is geen sprake van enige vorm van nabijheid of continuïteit tussen punten.
Opmerking. Een topologie op een verzameling \( X \) is een familie van deelverzamelingen (de “open verzamelingen”) die aan drie basisvoorwaarden voldoet:
- De lege verzameling en de gehele verzameling \( X \) behoren tot \( T \).
- Elke willekeurige vereniging van elementen van \( T \) behoort eveneens tot \( T \).
- Elke eindige doorsnede van elementen van \( T \) behoort ook tot \( T \).
We noemen deze topologie “discreet” omdat alle elementen van \( X \) volledig los van elkaar worden beschouwd. Er is geen enkel verband van nabijheid tussen de punten.
Het is de rijkste topologie die men op een verzameling kan definiëren, want geen enkele andere topologie bevat meer open verzamelingen: de discrete topologie bevat ze allemaal.
Opmerking. Deze regels vormen de basis van de topologie: ze beschrijven hoe we open verzamelingen kunnen combineren en vormen het formele kader voor het begrip continuïteit.
Open en gesloten tegelijk
Een opvallende eigenschap van de discrete topologie is dat elke deelverzameling zowel open als gesloten is.
Dat komt omdat alle deelverzamelingen open zijn, en het complement van een open verzameling in deze context dus ook open is. Volgens de definitie betekent dit dat elke deelverzameling tegelijk gesloten is.
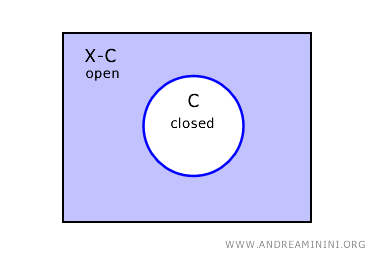
Met andere woorden: als het complement van een deelverzameling open is, dan is die deelverzameling zelf gesloten. Dit geldt voor alle mogelijke subsets van \( X \).
Daarom zegt men dat in de discrete topologie elke deelverzameling een clopen verzameling is - een verzameling die tegelijkertijd open en gesloten is.
Opmerking. Deze eigenschap geldt niet alleen voor afzonderlijke punten, maar voor elke denkbare deelverzameling. Elk punt en elke combinatie van punten is open. En omdat het complement daarvan ook weer een deelverzameling van \( X \) is, is die dus ook open en bijgevolg gesloten.
Een eenvoudig voorbeeld
Laten we dit concreet maken met een klein voorbeeld. Neem een verzameling \( X \) met drie elementen:
$$ X = \{a, b, c\} $$
De machtsverzameling van \( X \), dat wil zeggen alle mogelijke deelverzamelingen, bestaat uit:
- De lege verzameling: \(\emptyset\)
- De enkelvoudige verzamelingen: \(\{a\}\), \(\{b\}\), \(\{c\}\)
- De verzamelingen met twee elementen: \(\{a, b\}\), \(\{a, c\}\), \(\{b, c\}\)
- De volledige verzameling: \(\{a, b, c\}\)
In de discrete topologie is al deze verzamelingen open. De topologie \( T \) die op \( X \) wordt gedefinieerd, is dus:
$$ T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\} \} $$
Deze familie voldoet aan de regels van een topologie: ze bevat \( X \) en de lege verzameling en is stabiel onder willekeurige unies en eindige doorsneden.
Neem bijvoorbeeld de deelverzameling \( \{a\} \). Volgens de definitie is ze open. Het complement \( X \setminus \{a\} = \{b, c\} \) is eveneens open, dus is \( \{a\} \) ook gesloten. We zien dus dat in de discrete topologie elke deelverzameling tegelijkertijd open en gesloten is.
Hetzelfde geldt voor alle andere deelverzamelingen van \( X \).