Topologie van open verzamelingen
Een topologie T op een verzameling X is een collectie deelverzamelingen die we als open beschouwen. Zo’n collectie voldoet altijd aan twee basisregels:
- De lege verzameling ∅ en de volledige verzameling X zijn altijd open.
- Neem je een eindig aantal open verzamelingen en vorm je hun vereniging of doorsnede, dan krijg je opnieuw een open verzameling.
Met andere woorden, T bevat alleen deelverzamelingen van X die volgens de gekozen topologie open zijn. Bovendien blijft T stabiel onder vereniging en doorsnede.
Een collectie van verzamelingen is hier eenvoudigweg een verzameling waarvan de elementen zelf verzamelingen of deelverzamelingen zijn.
De combinatie van X en T vormt samen een topologische ruimte, genoteerd als (X,T). Dat is de basis waarop veel concepten uit de topologie verder worden opgebouwd.
Opmerking : In de praktijk zegt men vaak simpelweg dat “X een topologische ruimte is”. Maar formeel bestaat zo’n ruimte altijd uit twee elementen: de verzameling X en de topologie T, die bepaalt welke deelverzamelingen open zijn.
Waarom is de lege verzameling altijd open?
Dat is een keuze die de theorie overzichtelijk en consistent houdt. Dankzij deze conventie vermijdt men uitzonderingen in definities en bewijzen.
Voorbeeld
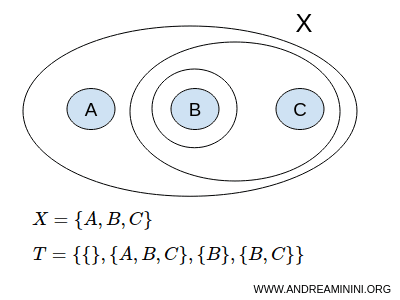
Neem de verzameling X met drie elementen A, B en C.
$$ X = \{ A,B,C \} $$
Een mogelijke topologie T op deze verzameling is:
$$ T = \{ \{ \},\{A,B,C\}, \{B\}, \{B,C\} \} $$
Hierin stelt { } de lege verzameling ∅ voor en {A,B,C} de volledige verzameling X. Zulke verzamelingen noemt men de improper subsets.
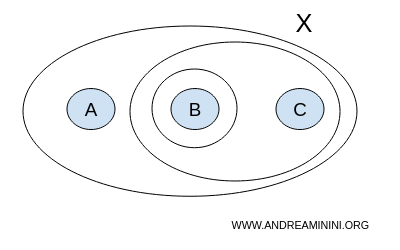
Een topologie bestaat enkel uit open verzamelingen. Daarom moeten vereniging en doorsnede van open verzamelingen opnieuw open zijn. In dit voorbeeld zie je dat dit steeds klopt. Enkele illustraties:
$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$
$$ \{ B \} \cup \{ A, B, C \} \subseteq \{ A, B, C \} \subseteq T$$
$$ \{ B \} \cup \{ \} \subseteq \{ B \} \subseteq T $$
$$ \{ B \} \cup \{ B \} \subseteq \{ B \} \subseteq T$$
En voor de doorsnede zien we hetzelfde gedrag:
$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ A, B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ \} \subseteq \{ \} \subseteq T $$
$$ \{ B \} \cap \{ B \} \subseteq \{ B \} \subseteq T$$
Omdat T gesloten blijft onder beide operaties, vormt het een geldige topologie op X.
Tweede voorbeeld
We gebruiken opnieuw dezelfde verzameling:
$$ X = \{ A,B,C \} $$
Maar nu voegen we {A} toe aan de eerdere collectie:
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
Dit lijkt misschien een kleine aanpassing, maar deze collectie is geen topologie. In een geldige topologie moet de vereniging van open verzamelingen opnieuw open zijn. Hier gaat het fout:
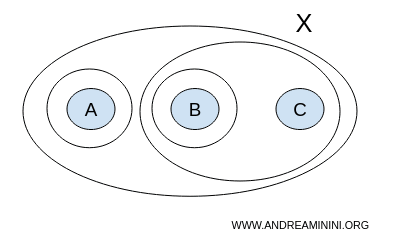
Neem bijvoorbeeld de vereniging van {A} en {B}. Dat levert {A,B}, maar deze verzameling zit niet in T:
$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\in} T $$
Hoewel {A} en {B} afzonderlijk open worden genoemd, is hun vereniging dat niet. Daarmee wordt een van de basisvoorwaarden overtreden en kunnen we deze collectie geen topologie noemen.
Dit toont hoe belangrijk de structuur van een topologie is en hoe sterk het begrip open verzameling afhangt van de gemaakte keuzes.