Normale topologische ruimte

Een topologische ruimte $ X $ heet normaal wanneer zij voldoet aan twee fundamentele voorwaarden:

Alle enkeltons zijn gesloten
Voor elk punt $ x \in X $ vormt de verzameling $\{x\}$ een gesloten deelverzameling.
Gescheiden gesloten verzamelingen kunnen worden gescheiden door open verzamelingen
Als twee gesloten verzamelingen $ A $ en $ B $ geen enkel punt gemeen hebben, dan bestaan er open verzamelingen $ U $ en $ V $ die respectievelijk $ A $ en $ B $ bevatten en elkaar nergens overlappen.

Het idee achter normaliteit is eenvoudig en krachtig: telkens wanneer twee gesloten verzamelingen volledig los van elkaar staan, kan de ruimte ze netjes uit elkaar houden met behulp van twee open verzamelingen die geen enkel raakpunt hebben.

Dit vermogen om verzamelingen topologisch scherp te scheiden is essentieel in veel klassieke resultaten, onder andere bij het construeren van continue functies die twee verzamelingen moeten onderscheiden. De stelling van Urysohn is daarvan een bekend voorbeeld.

Voorbeeld
Waarom dit belangrijk is

Voorbeeld

Neem de gebruikelijke topologie op de reële lijn $ \mathbb{R} $, gebaseerd op de open intervallen $ (a, b) $.

Beschouw twee gesloten verzamelingen die bovendien disjunct zijn:

$ A = \{0\} $
$ B = [2, 3] $

Deze twee verzamelingen zijn duidelijk gesloten en hebben geen enkel punt gemeenschappelijk.

schematische weergave van disjuncte gesloten verzamelingen op de reële lijn

Opmerking. Een enkelton zoals $ A $ is altijd gesloten. Het interval $ B $ is gesloten volgens de standaarddefinitie in $ \mathbb{R} $.

We zoeken nu twee open verzamelingen die $ A $ en $ B $ elk afzonderlijk bevatten en elkaar niet overlappen.

Voor $ A $ ligt het open interval $ U = (-1, 1) $ voor de hand:

$$ A \subset U = (-1,1) $$

Voor $ B $ kunnen we eenvoudig het open interval $ V = (1, 4) $ nemen:

$$ B \subset V = (1,4) $$

Deze twee open verzamelingen snijden elkaar niet, omdat $ (-1, 1) $ strikt links ligt van $ (1, 4) $. Daarmee is de scheiding compleet.

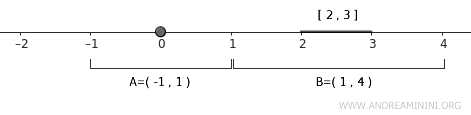
open intervallen die twee gesloten verzamelingen strikt scheiden

Dit voorbeeld toont precies wat normaliteit inhoudt: gesloten verzamelingen die uit elkaar liggen, kunnen altijd worden gescheiden door open verzamelingen. In $ \mathbb{R} $ werkt dit mechanisme zelfs bijzonder soepel, dankzij de metrische structuur van de ruimte.

Waarom dit belangrijk is

Normale ruimtes spelen een belangrijke rol in de topologie, en veel theorieën zijn er expliciet op gebaseerd. Enkele kernpunten:

De reële lijn $ \mathbb{R} $ is normaal
Bovendien is zij regulier en zelfs volledig normaal, wat de basis vormt voor veel functionele scheidingstechnieken.
Elke metrische ruimte is normaal
Door de aanwezigheid van een metriek kan men open bollen gebruiken om gesloten verzamelingen netjes te scheiden.
Normaliteit impliceert regulariteit
Wie normaliteit heeft, beschikt automatisch over een sterkere vorm van scheiding tussen punten en gesloten verzamelingen, al geldt het omgekeerde niet altijd.

Normaliteit is dus een van de pijlers van de topologie. Ze biedt de benodigde structuur om verfijnde scheidingstechnieken, continue functies en verdere theoretische bouwstenen mogelijk te maken.