De basis van een topologie
Een basis van een topologie is een verzameling \( B \) van open verzamelingen waarmee je alle open verzamelingen van een topologie \( T \) kunt opbouwen. Elke open verzameling kan dus worden gezien als een unie van elementen uit \( B \).
Neem een verzameling \( X \) waarop een collectie \( T \) van deelverzamelingen een topologie vormt. Een basis van deze topologie is dan een verzameling \( B \) van zogenoemde basisverzamelingen. Die basis moet aan twee voorwaarden voldoen:
- Ieder element \( x \in X \) behoort tot minstens één basisverzameling.
- Als twee basisverzamelingen elkaar snijden in een punt \( x \), dan moet er binnen hun doorsnede opnieuw een basisverzameling liggen die dat punt bevat.
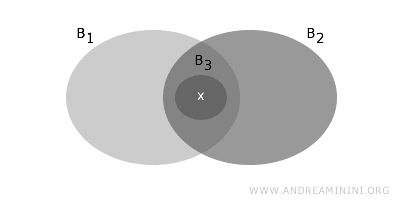
Dankzij deze twee eisen kun je vanuit de basis alle open verzamelingen van de topologie reconstrueren.
Waarom is een basis zo handig?
Een topologie bestaat vaak uit een groot aantal open verzamelingen. Door met een basis te werken hoef je niet al deze open verzamelingen afzonderlijk te beschrijven. Je geeft enkel de basisverzamelingen, en alle overige open verzamelingen volgen automatisch door unions te nemen.
Opmerking: De doorsnedeeis zorgt ervoor dat de topologie zich netjes gedraagt. In het bijzonder blijft de doorsnede van twee open verzamelingen open.
Een eenvoudig voorbeeld
Neem de verzameling:
$$ X = \{a, b, c \} $$
met de topologie:
$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$
Een bijpassende basis is:
$$ B = \{ \{ a \}, \{ b,c \} \} $$
Deze basis werkt omdat elk element van \( X \) ergens in voorkomt en omdat elke open verzameling uit \( T \) kan worden geschreven als een unie van basisverzamelingen.
Voorbeelden:
- \( \{a\} \) is al een basisverzameling.
- \( \{b,c\} \) eveneens.
- \( \{a,b,c\} = \{a\} \cup \{b,c\} \).
Opmerking: De lege verzameling behoort standaard tot elke topologie: $$ \emptyset \in T $$
Dit voorbeeld laat goed zien hoe een basis in een klein, overzichtelijk domein werkt. Voor grotere of oneindige verzamelingen wordt het wat abstracter, maar het principe blijft precies hetzelfde.
Een alternatieve basis
We kunnen dezelfde topologie ook genereren met een andere basis, bijvoorbeeld:
$$ B = \{ \{ a \}, \{ b \}, \{ c \} \} $$
Dit zijn de singletons van \( X \). Hiermee krijgen we opnieuw alle open verzamelingen:
- \( \varnothing \) is altijd open.
- \( \{a\} \) is al een element van \( B \).
- \( \{b,c\} = \{b\} \cup \{c\} \).
- \( X = \{a\} \cup \{b\} \cup \{c\} \).
Opmerking: Dit laat mooi zien dat een topologie meerdere mogelijke bases kan hebben. De structuur blijft dezelfde, maar de manier waarop je haar opbouwt kan verschillen.
Voorbeeld 2: de reële rechte
Op de reële lijn \( \mathbb{R} \) gebruiken we meestal de natuurlijke basis:
$$ B = \{ (a,b) \subseteq \mathbb{R} \mid a < b \} $$
Elk punt ligt in talloze open intervallen en de doorsnede van twee intervallen die hetzelfde punt bevatten levert altijd weer een kleiner open interval op. Daarmee voldoet deze familie aan beide basisvoorwaarden.
Voorbeeld: \( (0,3) \) en \( (2,4) \) hebben als doorsnede \( (2,3) \), dat opnieuw in \( B \) zit.
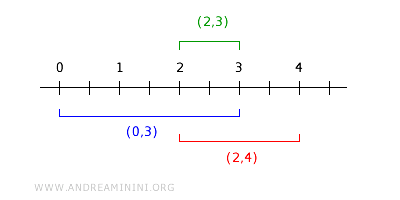
We zien dus dat: $$ (0,3) \cap (2,4) = (2,3) \in B $$
Enkele laatste beschouwingen
Een basis die alle singletons van een verzameling bevat, kan heel uiteenlopende topologieën genereren. Door unions van singletons te nemen ontstaan bijvoorbeeld:
- Topologieën waarin sommige elementen wel en andere niet als open singletons verschijnen.
- De triviale topologie \( T = \{ \varnothing, X \} \).
- De discrete topologie, waarin alle deelverzamelingen open zijn.
Opmerking: De twee basisvoorwaarden zijn in dit geval automatisch vervuld. Elke singleton bevat precies één element en singletons overlappen niet.
Dit idee werkt in elke context, van kleine eindige verzamelingen tot grote en complexe ruimtes. Een basis biedt steeds een compacte, begrijpelijke manier om een topologie op te bouwen en te analyseren.