Open verzamelingen in de topologie

Een verzameling A heet open wanneer voor elk element x in A (x∈A) een omgeving van x bestaat die volledig in A is opgenomen.
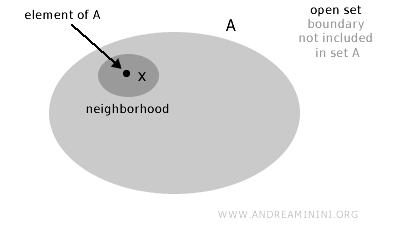
voorbeeld van een open verzameling

Met andere woorden, een verzameling heet open als de rand intuïtief niet tot de verzameling zelf behoort.

Formeel geldt dat een verzameling A in een topologische ruimte X open is wanneer voor ieder punt x in A een omgeving bestaat die geheel binnen A ligt.

Opmerking. Dit betekent dat rond ieder punt uit de verzameling een kleine regio te vinden is die volledig tot A behoort en de buitenrand niet raakt.

Een eerste voorbeeld
Het kiezen van een topologie
Stelling over open verzamelingen

Een eerste voorbeeld

Een klassiek voorbeeld van een open verzameling op de reële lijn is een open interval.

Wat is een open interval? Een open interval in R is de verzameling reële getallen x waarvoor a < x < b, met a en b twee reële getallen waarvoor a < b.

We noteren dit als (a,b). De ronde haken geven aan dat de grenspunten a en b niet tot het interval behoren.

Zo is het open interval (3,10) een open verzameling op de reële as.

Dit interval bevat oneindig veel reële getallen tussen 3 en 10, zonder de uiteinden zelf.

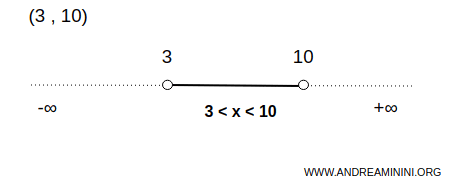
voorbeeld van een open interval

Voor elk punt x in dit interval bestaat er een kleiner open interval dat volledig in (3,10) ligt.

Neem bijvoorbeeld x=3.1. We kunnen dan het open interval (3.09,3.11) kiezen, dat geheel binnen (3,10) valt.

Dit geldt voor elk ander punt in (3,10), want tussen twee reële getallen liggen altijd oneindig veel andere reële getallen.

Opmerking. Zelfs bij een zeer kleine marge, bijvoorbeeld rond 3.001, kunnen we een omgeving nemen zoals 3.001±0.00000001, met opnieuw oneindig veel punten die allemaal binnen (3,10) blijven.

Dit vormt een eenvoudig eendimensionaal voorbeeld van een open verzameling.

Voorbeelden in hogere dimensies

Hetzelfde idee geldt in twee dimensies, bijvoorbeeld in het vlak.

Beschouw de verzameling van alle punten binnen een cirkel met straal r=1 en middelpunt in de oorsprong (0,0).

$$ x^2+y^2<1 $$

Deze ongelijkheid beschrijft alle punten waarvan de afstand tot het middelpunt kleiner is dan 1. De punten op de cirkelrand horen er dus niet bij, alleen de binnenzijde.

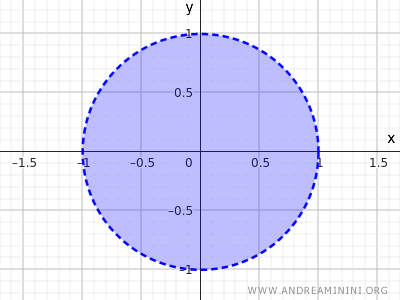
open verzameling in het vlak

Dit is opnieuw een voorbeeld van een open verzameling.

Wanneer is een verzameling gesloten?

Een verzameling wordt gesloten als we ook de punten op de cirkelrand meenemen.

$$ x^2+y^2 \le 1 $$

In dat geval geldt niet meer dat ieder punt een omgeving heeft die volledig binnen de verzameling blijft.

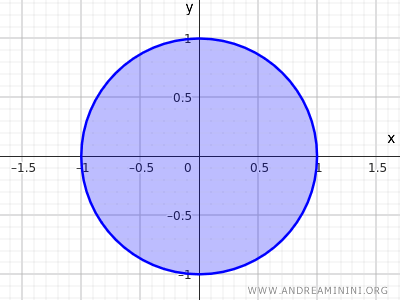
voorbeeld van een gesloten verzameling in het vlak

Punten op de rand beschikken niet over een omgeving die in zijn geheel binnen de verzameling ligt.

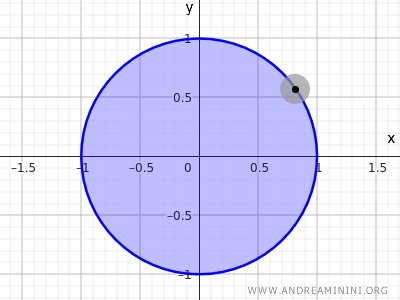
gesloten verzameling met grenspunten

Opmerking. In R² is de vergelijking $ x^2+y^2=1 $ op zichzelf noch een open noch een gesloten verzameling, omdat zij uitsluitend de rand beschrijft. De ongelijkheid $ x^2+y^2<1 $ geeft een open verzameling, terwijl $ x^2+y^2\le 1 $ een gesloten verzameling oplevert.

In drie dimensies werkt dit precies hetzelfde. Een open bol verkrijgt men door alle punten binnen de bol te nemen en de boloppervlakte weg te laten.

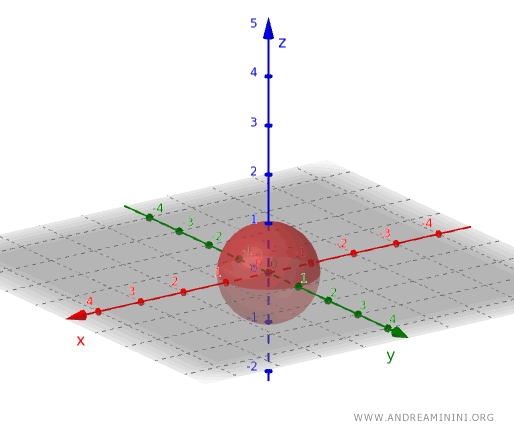
open verzameling in drie dimensies

Het kiezen van een topologie

Open intervallen zijn nuttig omdat ze het idee van openheid intuïtief maken.

Toch is het begrip open verzameling veel algemener en mag het niet uitsluitend met zulke voorbeelden worden vereenzelvigd.

Wie het concept eenmaal begrijpt, kan het verder abstraheren.

Het begrip openheid hangt volledig af van de topologie die op een ruimte wordt gelegd.

De definitie van open verzamelingen kan sterk verschillen afhankelijk van de gekozen topologie.

Een verzameling die in de standaardtopologie gesloten lijkt, kan in een andere topologie open zijn.

Met andere woorden: of een verzameling open is, hangt uitsluitend af van de gekozen topologie.

Wat is een topologie? Een topologie op een ruimte is een collectie verzamelingen die als open worden beschouwd en die voldoet aan bepaalde axioma’s. Zo moet de unie van willekeurig veel open verzamelingen open blijven en de doorsnede van eindig veel open verzamelingen eveneens open zijn.

Daarom is het zinvol om verder te kijken dan uitsluitend de meest vertrouwde voorbeelden zoals open intervallen of open schijven.

In de topologie is de verzameling open verzamelingen vaak veel rijker dan men op het eerste gezicht zou vermoeden.

Een illustratief voorbeeld

Neem de ruimte $ \{a, b\} $, bestaande uit slechts twee elementen.

Op deze ruimte kunnen minimaal twee verschillende topologieën worden gedefinieerd: de triviale topologie en de discrete topologie.

Triviale topologie
In deze topologie zijn alleen de lege verzameling $ \emptyset $ en de volledige ruimte $ \{a, b\} $ open. Dit is de eenvoudigste mogelijke topologie, met minimale structuur.
Discrete topologie
In deze topologie is elke deelverzameling van $ \{a, b\} $ open. Dus $ \{a\} $, $ \{b\} $, $ \{a, b\} $ en $ \emptyset $ zijn allemaal open. Dit is de meest gedetailleerde topologie, waarin elke combinatie van punten een open verzameling vormt.

Bekijken we nu de verzameling $ \{a\} $ binnen beide topologieën:

In de triviale topologie is {a} niet open
De enige open verzamelingen met elementen zijn $ \{a, b\} $ en $ \emptyset $.
In de discrete topologie is {a} wel open
Daar is elke deelverzameling van $ \{a, b\} $ per definitie open.

De verzameling $ \{a\} $ is dus open in de discrete topologie, maar niet in de triviale topologie.

Dit voorbeeld onderstreept hoe sterk het begrip openheid afhangt van de gekozen topologie.

Stelling over open verzamelingen

Stelling 1

Gegeven een open verzameling X met een topologie T die samen de topologische ruimte (X,T) vormen, dan is een deelverzameling S⊂X een open verzameling in (X,T) als ieder element (punt) s∈S een omgeving U heeft die volledig in S ligt, dus U⊂S.

Per definitie is S een open verzameling omdat zij behoort tot de topologische ruimte (X,T).

De deelverzameling S kan daardoor worden opgevat als de omgeving van elk van haar punten s∈S.

Hieruit volgt dat iedere omgeving U_s van een element s∈S zelf een open verzameling is die in S besloten ligt.

$$ x \in U_s \subset S \subset X $$

Een open verzameling kan worden beschouwd als de unie van de open omgevingen van haar punten.

Als dus ieder element s∈S een omgeving U_s heeft met U_s⊂S, dan volgt dat S een open verzameling is, aangezien zij kan worden opgevat als de unie van open verzamelingen.

Met andere woorden, een verzameling is open dan en slechts dan als ieder punt erin een omgeving heeft die geheel binnen die verzameling ligt.

Voorbeeld. Stel een tafel voor met glazen knikkers. Elke knikker stelt een punt binnen een verzameling voor. Een verzameling noemen we "open" als er rond elke knikker voldoende ruimte bestaat om vrij te bewegen zonder de tafelrand te raken. Wanneer rond elke knikker een cirkel kan worden getrokken die volledig op het tafelblad blijft zonder de randen te raken, dan vertegenwoordigt de hele configuratie een open verzameling. De essentie is dat, ongeacht welke knikker wordt gekozen, er altijd een zone om haar heen bestaat die nog volledig tot de verzameling behoort.
voorbeeld van een open verzameling met knikkers op een tafel

Stelling 2

Neem een verzameling $ X $ en een basis $ B $ voor een topologie op $ X $. Een deelverzameling $ A \subset X $ is open in de door $ B $ geïnduceerde topologie dan en slechts dan als voor ieder element $ x \in A $ een basisverzameling $ B_x $ bestaat waarvoor $ x \in B_x $ en $ B_x \subseteq A $.

Deze stelling benadrukt een fundamentele eigenschap van topologieën die worden opgebouwd uit een basis.

Met andere woorden, ieder punt van $ A $ moet een omgeving hebben, $ B_x $, die tot de basis behoort en volledig binnen $ A $ ligt.

Daarmee wordt bevestigd dat $ A $ werkelijk open is in de door $ B $ voortgebrachte topologie.

Bewijs. Als $ A $ open is in de door de basis $ B $ gegenereerde topologie op $ X $, dan is $ A $ per definitie de unie van basisverzamelingen. Elk element $ x \in A $ behoort dus tot ten minste één basisverzameling $ B_x $ die volledig in $ A $ is opgenomen. Het omgekeerde geldt eveneens: als voor elk punt $ x \in A $ een basisverzameling $ B_x \subseteq A $ bestaat, dan is $ A $ open in de topologie die door $ B $ wordt opgewekt.

Voorbeeld

Neem $ X = \{1, 2, 3, 4, 5\} $ en de basis $ B = \{\{1\}, \{2, 3\}, \{4, 5\}\} $. We onderzoeken of de deelverzameling $ A = \{1, 2, 3\} $ open is.

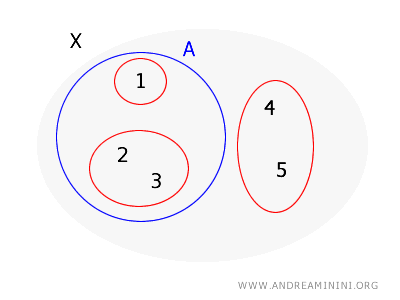
voorbeeld van een open deelverzameling in een topologie

Voor elk punt in $ A $ moet een basisverzameling bestaan die het bevat en volledig in $ A $ ligt:

Voor $ 1 $ is er de basisverzameling $ \{1\} $, die geheel in $ A $ ligt.
Voor $ 2 $ is er de basisverzameling $ \{2, 3\} $, die volledig in $ A $ ligt.
Voor $ 3 $ geldt hetzelfde: $ \{2, 3\} $ bevat ook $ 3 $ en ligt in zijn geheel binnen $ A $.

Aangezien elk punt in $ A $ is opgenomen in een basisverzameling die volledig binnen $ A $ ligt, wordt aan de voorwaarde van de stelling voldaan.

Daarom volgt dat $ A $ een open verzameling is in de door $ B $ bepaalde topologie.

Voorbeeld 2

Beschouw opnieuw $ X = \{1, 2, 3, 4, 5\} $ met dezelfde basis $ B = \{\{1\}, \{2, 3\}, \{4, 5\}\} $.

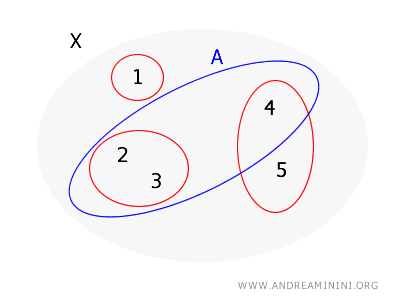
voorbeeld van een deelverzameling die niet open is

We onderzoeken nu of $ A = \{2, 3, 4\} $ open is.

Voor $ 2 $ kan de basisverzameling $ \{2, 3\} $ worden gebruikt. Die ligt volledig in $ A $.
Voor $ 3 $ geldt hetzelfde, aangezien $ \{2, 3\} $ ook dat element volledig dekt.
Voor $ 4 $ bestaat echter geen basisverzameling die zowel $ 4 $ bevat als volledig binnen $ A $ ligt. De enige basisverzameling die $ 4 $ bevat is $ \{4, 5\} $, maar deze bevat ook $ 5 $, dat niet tot $ A $ behoort.

Daarom is $ A $ geen open verzameling in de door $ B $ geïnduceerde topologie, omdat niet ieder punt in $ A $ een basisverzameling heeft die volledig in $ A $ ligt.

Hetzelfde redeneringsprincipe kan verder worden toegepast op andere voorbeelden.