Rand van een verzameling

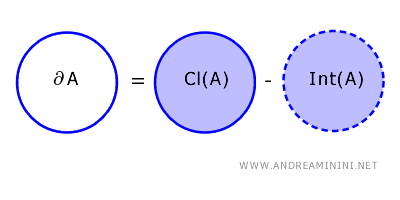
De rand van een deelverzameling $ A $ van een topologische ruimte $ X $ bestaat uit alle punten die wel tot de afsluiting van $ A $ behoren, maar niet tot het inwendige ervan : \[ \partial A = \text{Cl}(A) - \text{Int}(A) \]

Hierbij staat $ \text{Cl}(A) $ voor de afsluiting van $ A $. Deze bevat niet alleen de punten van $ A $ zelf, maar ook alle punten die als limietpunt met $ A $ samenhangen.

Daartegenover staat $ \text{Int}(A) $, het inwendige van $ A $. Dit is de verzameling van alle punten waarvoor een open omgeving bestaat die volledig binnen $ A $ ligt.

voorbeeld van de rand van een verzameling binnen een topologische ruimte

Een belangrijk punt is dat de rand geen vaste eigenschap van een verzameling op zichzelf is. Ze hangt altijd af van de topologie die men op de ruimte kiest.

Daardoor kan dezelfde verzameling, bekeken binnen verschillende topologische structuren, verschillende randen hebben.

Kort gezegd bestaat de rand van een verzameling $ A $ uit precies die punten die tegelijkertijd in de nabijheid liggen van $ A $ en van haar complement $ X \setminus A $.

Een concreet voorbeeld
Randstelling
Opmerkingen

Een concreet voorbeeld

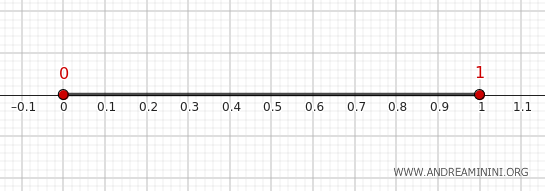
Neem de verzameling $ A = (0, 1) $, beschouwd als deelverzameling van de reële rechte $ \mathbb{R} $ met haar gebruikelijke topologie.

We bepalen nu stap voor stap de rand van deze verzameling.

1] Afsluiting van A

De afsluiting van $ A $, genoteerd als $ \text{Cl}(A) $, omvat alle punten van $ A $ en alle bijbehorende ophopingspunten.

Voor $ A = (0, 1) $ is de afsluiting het gesloten interval $[0, 1]$. De punten 0 en 1 zijn namelijk limietpunten van $ A $, net zoals alle punten tussenin.

$$ \text{Cl}(A) = [0, 1] $$

2] Inwendige van A

Het inwendige van $ A $, aangeduid met $ \text{Int}(A) $, bestaat uit alle punten waarvoor een open omgeving volledig in $ A $ vervat is.

Aangezien $ A = (0, 1) $ zelf een open interval is, valt het inwendige samen met de verzameling:

$$ \text{Int}(A) = (0, 1) $$

3] Rand van A

De rand van $ A $, genoteerd als $ \partial A $, verkrijgt men door het inwendige van $ A $ te verwijderen uit de afsluiting:

$$ \partial A = \text{Cl}(A) - \text{Int}(A) $$

Door de gevonden resultaten in te vullen, volgt:

$$ \partial A = [0, 1] - (0, 1) = \{0, 1\} $$

In de gebruikelijke topologie van $ \mathbb{R} $ bestaat de rand van de verzameling $ A = (0,1) $ dus uit de twee punten $\{0, 1\}$.

Deze punten liggen letterlijk op de grens van de verzameling, omdat elke open omgeving van 0 of 1 zowel punten van $ A $ als van het complement $ X \setminus A $ bevat.

schematische weergave van de rand van een deelverzameling van de reële rechte

Randstelling

Een punt $ x \in X $ behoort tot de rand $ \partial A $ van een deelverzameling $ A $ dan en slechts dan wanneer elke open omgeving van $ x $ zowel $ A $ als haar complement $ X - A $ snijdt.

Deze stelling biedt een praktisch criterium: om te bepalen of een punt $ x $ op de rand van $ A $ ligt, volstaat het te controleren dat elke open omgeving van $ x $ tegelijkertijd elementen van $ A $ en van $ X - A $ bevat.

Voorbeeld

We nemen opnieuw de verzameling $ A = (0, 1) $, opgevat als deelverzameling van $ \mathbb{R} $ met de standaardtopologie.

In dit geval geldt:

$$ \text{Cl}(A) = [0, 1] \quad \text{en} \quad \text{Int}(A) = (0, 1) $$

Daaruit volgt meteen dat de rand van $ A $ gelijk is aan:

$$ \partial A = \{0, 1\} $$

We controleren nu stap voor stap dat deze punten inderdaad voldoen aan het criterium van de randstelling.

1] Controle voor het punt 0

Beschouw een open omgeving van 0, bijvoorbeeld het interval $ (0 - \epsilon, 0 + \epsilon) $ met $ \epsilon > 0 $.

Deze omgeving snijdt de verzameling $ A $, omdat zij punten van het interval $ (0, 1) $ bevat. Tegelijkertijd snijdt zij ook het complement $ X - A $, aangezien zij punten kleiner dan of gelijk aan 0 bevat.

Daarom behoort het punt 0 tot de rand:

$ 0 \in \partial A $.

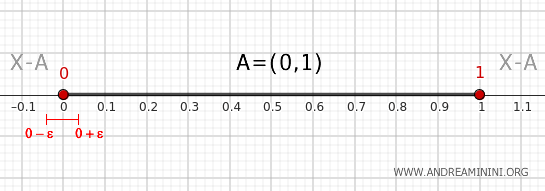
open omgeving van het punt 0 op de reële rechte

2] Controle voor het punt 1

Neem nu een open omgeving van 1, bijvoorbeeld het interval $ (1 - \epsilon, 1 + \epsilon) $.

Ook deze omgeving snijdt zowel $ A $, doordat zij punten van $ (0,1) $ bevat, als het complement $ X - A $, omdat zij punten groter dan of gelijk aan 1 omvat.

Bijgevolg geldt ook hier:

$ 1 \in \partial A $.

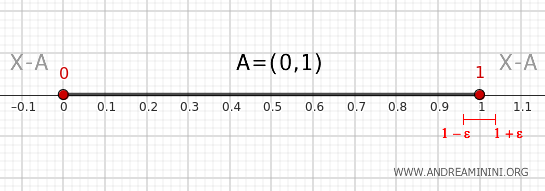
open omgeving van het punt 1 op de reële rechte

3] Controle voor een inwendig punt

Kies nu een willekeurig punt in het interval $ (0,1) $, bijvoorbeeld 0,5.

Elke open omgeving van 0,5 ligt volledig binnen $ A $ en kan dus geen enkel punt van het complement $ X - A $ bevatten.

Daaruit volgt:

$ 0.5 \notin \partial A $.

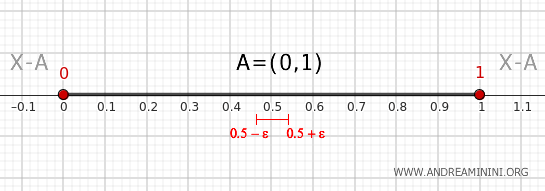
open omgeving van het inwendige punt 0,5

Samengevat bevestigt de randstelling dat de punten 0 en 1 daadwerkelijk tot de rand van $ A = (0, 1) $ behoren, terwijl een punt zoals 0,5 geen randpunt is. De rand van $ A $ is dus precies de verzameling $\{0, 1\}$.

Opmerkingen

We sluiten af met enkele belangrijke en vaak gebruikte eigenschappen van randen in de topologie.

De rand $ \partial A $ is vervat in $ A $ dan en slechts dan wanneer $ A $ gesloten is:
\[ \partial A \subseteq A \Leftrightarrow A \text{ is gesloten} \]
De rand $ \partial A $ en $ A $ zijn disjunct dan en slechts dan wanneer $ A $ open is:
Met andere woorden: $ A $ is open precies wanneer geen enkel punt van $ A $ op zijn rand ligt.
\[ \partial A \cap A = \emptyset \Leftrightarrow A \text{ is open} \]
De rand $ \partial A $ is leeg dan en slechts dan wanneer $ A $ zowel open als gesloten is (clopen):
\[ \partial A = \emptyset \Leftrightarrow A \text{ is clopen} \]
De rand $ \partial A $ kan worden beschreven als de doorsnede van de afsluiting van $ A $ met die van haar complement:
\[ \partial A = \text{Cl}(A) \cap \text{Cl}(X - A) \]
De rand $ \partial A $ is altijd een gesloten verzameling:

De doorsnede van twee gesloten verzamelingen is opnieuw gesloten. Omdat $ \partial A $ gedefinieerd is als $\text{Cl}(A) \cap \text{Cl}(X - A)$, volgt hieruit dat de rand altijd een gesloten deelverzameling is.
De rand en het inwendige van een verzameling zijn altijd disjunct:
\[ \partial A \cap \text{Int}(A) = \emptyset \]
De vereniging van het inwendige en de rand is gelijk aan de afsluiting van de verzameling:
\[ \partial A \cup \text{Int}(A) = \text{Cl}(A) \]

Enzovoort.