De grens van een verzameling

Een punt $ x $ behoort tot de grens van een verzameling $ A $ wanneer elke omgeving van $ x $ zowel punten van $ A $ als punten van het complement $ X - A $ bevat.

Intuïtief betekent dit dat men rond $ x $ nooit een omgeving kan vinden die volledig in $ A $ ligt, maar ook geen omgeving die volledig buiten $ A $ ligt. In dat geval bevindt $ x $ zich precies op de scheidingslijn tussen de verzameling en haar complement.

Een concreet voorbeeld
Het bewijs

Een concreet voorbeeld

We illustreren dit begrip aan de hand van een eenvoudig en bekend voorbeeld.

Neem de verzameling $ A = (0, 1) $ op de reële getallenlijn $ \mathbb{R} $.

De punten 0 en 1 behoren tot de grens van $ A $. Welke omgeving men ook rond deze punten kiest, men vindt altijd zowel punten die tot het interval $ (0, 1) $ behoren als punten die erbuiten liggen.

Punt 1
Elke omgeving van de vorm $ (1 - \epsilon, 1 + \epsilon) $, met ε willekeurig klein, bevat een deel $ (1 - \epsilon, 1) $ dat in $ A $ ligt en een deel $ (1, 1 + \epsilon) $ dat buiten $ A $ ligt. Het punt 1 is dus een grenspunt van $ A $.
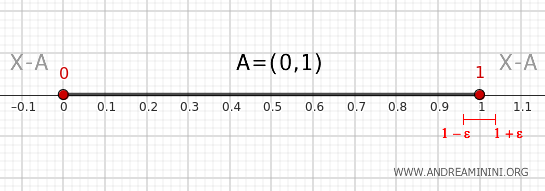
Punt 0
Op dezelfde manier bevat elke omgeving $ (0 - \epsilon, 0 + \epsilon) $ een deel $ (0, 0 + \epsilon) $ dat in $ A $ ligt en een deel $ (0 - \epsilon, 0) $ dat tot het complement behoort. Ook het punt 0 is dus een grenspunt van $ A $.
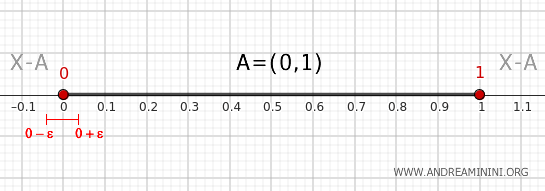
Inwendig punt van het interval (0, 1)
Elk punt $ x $ dat strikt tussen 0 en 1 ligt, heeft een omgeving $ (x - \epsilon, x + \epsilon) $ met ε > 0 die volledig in $ A $ is opgenomen. Zo’n omgeving snijdt het complement niet, waardoor deze punten geen deel uitmaken van de grens.
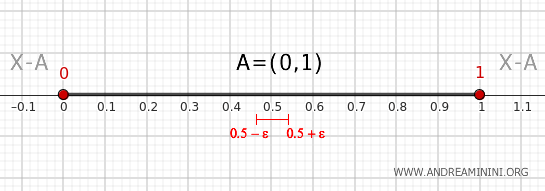
Punt buiten het interval (0, 1)
Elk punt dat strikt buiten het interval $ (0, 1) $ ligt, met uitzondering van de punten 0 en 1, heeft een omgeving $ (x - \epsilon, x + \epsilon) $ die volledig in $ X - A $ ligt en geen enkel punt van $ A $ bevat. Deze punten behoren dus niet tot de grens.

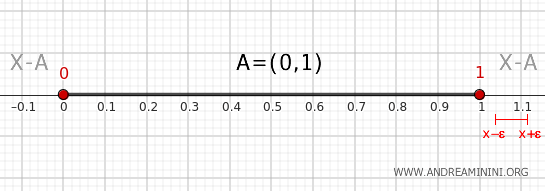
We concluderen dat de grens van $ A $ precies uit de punten 0 en 1 bestaat:

$$ \partial A = \{0,1 \} $$

Kort samengevat is een punt $ x $ een grenspunt van $ A $ als geen enkele omgeving van $ x $ volledig in $ A $ ligt en ook geen enkele volledig in het complement. Dit criterium vormt een praktisch en helder hulpmiddel om grenspunten te herkennen.

Het bewijs

We bewijzen deze karakterisering door twee implicaties te beschouwen.

1] Veronderstel dat $ x \in \partial A $

Volgens de definitie geldt dan:

$$ x \in \text{Cl}(A) \quad \text{en} \quad x \notin \text{Int}(A) $$

Uit $ x \in \text{Cl}(A) $ volgt dat elke omgeving van $ x $ minstens één punt van $ A $ bevat.

De voorwaarde $ x \notin \text{Int}(A) $ betekent dat geen enkele omgeving van $ x $ volledig in $ A $ ligt. Elke omgeving bevat dus noodzakelijk ook punten van het complement $ X - A $.

Daaruit volgt dat elke omgeving van $ x $ zowel $ A $ als $ X - A $ snijdt.

2] Veronderstel dat elke omgeving van $ x $ zowel $ A $ als $ X - A $ snijdt

Dan behoort $ x $ per definitie tot zowel $ \text{Cl}(A) $ als $ \text{Cl}(X - A) $.

Aangezien $ \text{Cl}(X - A) = X - \text{Int}(A) $, volgt hieruit dat $ x \notin \text{Int}(A) $.

We verkrijgen dus:

$$ x \in \text{Cl}(A) \setminus \text{Int}(A) = \partial A $$

Daarmee is ook de omgekeerde richting aangetoond en is de karakterisering van de grens volledig bewezen.