Homeomorfismen in de topologie

Een homeomorfisme is een topologische transformatie die wordt beschreven door een functie die zowel bijectief als continu is, en waarvan ook de inverse continu is.

In meer beeldende termen maakt een homeomorfisme het mogelijk een ruimte om te vormen tot een andere en vervolgens weer terug te keren naar de oorspronkelijke toestand, zonder te scheuren of iets toe te voegen.

Eenvoudig gezegd zorgt een homeomorfisme voor een vloeiende overgang van de ene ruimte naar de andere, zonder de topologische eigenschappen te veranderen.

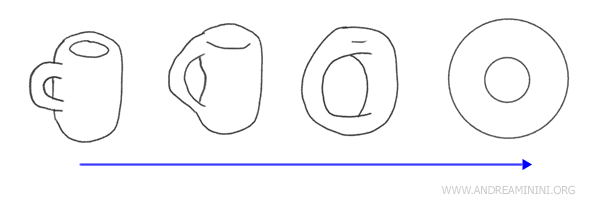
Neem bijvoorbeeld een koffiekop met een oor en een donut (torus) - deze objecten zijn topologisch homeomorf. Het ene kan namelijk door een continue vervorming in het andere worden omgezet, en omgekeerd.

Topologisch gezien zijn deze vormen equivalent omdat ze elk precies één "gat" hebben - het gat in de donut en de opening van het oor van de kop. Door de kop geleidelijk rond het oor te vervormen, kan ze de vorm van een donut aannemen.

Wanneer twee topologische ruimten door een homeomorfisme met elkaar verbonden zijn, noemt men ze homeomorfe ruimten. Dat betekent dat ze, vanuit topologisch oogpunt, fundamenteel dezelfde structuur hebben, ook al kunnen hun geometrische vormen sterk verschillen.

Kenmerken van een homeomorfisme

Een homeomorfisme heeft een aantal essentiële eigenschappen:

• Bijectiviteit
  Elk punt van de ene ruimte komt op unieke wijze overeen met precies één punt van de andere, en omgekeerd.
• Continuïteit
  Een homeomorfisme is per definitie een continue afbeelding: kleine veranderingen in de invoer veroorzaken kleine veranderingen in de uitvoer.
• Continue inverse
  De inverse van de afbeelding moet eveneens continu zijn. Dit garandeert dat de transformatie omkeerbaar is zonder de continuïteit te verbreken.
• Behoud van topologische eigenschappen
  Een homeomorfisme behoudt de fundamentele topologische eigenschappen zoals continuïteit, samenhang en compactheid. De onderlinge relaties binnen de oorspronkelijke ruimte blijven daardoor intact in de getransformeerde ruimte.

Samengevat is een homeomorfisme een continue, bijectieve afbeelding tussen twee topologische ruimten \(X\) en \(Y\), waarvan ook de inverse continu is. Daardoor blijven de topologische eigenschappen van beide ruimten behouden.

Kortom, een homeomorfisme maakt het mogelijk een ruimte te herschikken tot een andere zonder te scheuren of te lijmen: het is een vorm van volledige topologische equivalentie tussen twee ruimtelijke structuren.

We herinneren ons de topologische definitie van continuïteit:

Laat \(X\) en \(Y\) twee topologische ruimten zijn. Een afbeelding \(f : X \to Y\) heet continu als voor elke open verzameling \(V\) in \(Y\) het inverse beeld \(f^{-1}(V)\) een open verzameling in \(X\) is.

Met andere woorden: een continue afbeelding in de topologie behoudt de structuur van de open verzamelingen bij de overgang van de ene ruimte naar de andere.

Het begrip continuïteit in de topologie is dus abstracter en algemener dan in de analyse.

Opmerking: In de analyse berust continuïteit op de afstand tussen punten. In de topologie steunt ze uitsluitend op de structuur van open verzamelingen, zonder verwijzing naar afstand.

Een concreet voorbeeld

Laten we de begrippen continuïteit en homeomorfisme op een heldere en intuïtieve manier illustreren met behulp van open verzamelingen.

Beschouw twee topologische ruimten: \(X = \{a, b, c, d\}\) en \(Y = \{1, 2\}\).

• In de ruimte \(X\) zijn de open verzamelingen: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
• In de ruimte \(Y\) zijn de open verzamelingen: \(\{\}, \{1\}, \{1, 2\}\).

Een afbeelding \(f : X \to Y\) is continu als voor elke open verzameling in \(Y\) het inverse beeld een open verzameling in \(X\) is.

We definiëren \(f\) als volgt:

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).

Om dit inzichtelijk te maken, tonen we de afbeelding \(f\) en de topologische ruimten door de open verzamelingen met cirkels aan te duiden.

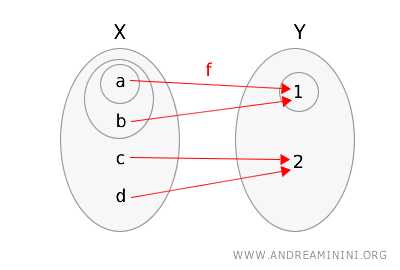
We controleren nu de topologische definitie van continuïteit:

• De open verzameling \(\{1\}\) in \(Y\) heeft als inverse beeld \(f^{-1}(\{1\}) = \{a, b\}\), dat open is in \(X\).
• De open verzameling \(\{1, 2\}\) in \(Y\) heeft als inverse beeld \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\), dat eveneens open is in \(X\).

Aangezien het inverse beeld van elke open verzameling in \(Y\) open is in \(X\), is de afbeelding \(f\) continu.

Opmerking: De lege verzameling wordt niet vermeld omdat ze per definitie open is in elke topologische ruimte.

Beschouw nu een andere afbeelding \(g : X \to Y\), gedefinieerd als:

\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\).

Ook deze afbeelding wordt grafisch weergegeven door de open verzamelingen te omcirkelen.

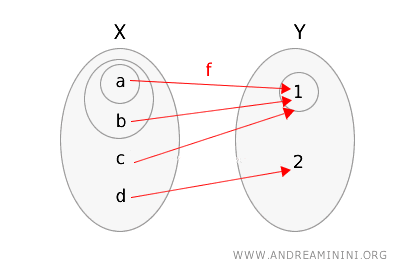
Controle van de continuïteit:

• De open verzameling \(\{1\}\) in \(Y\) heeft als inverse beeld \(g^{-1}(\{1\}) = \{a, b, c\}\), dat niet open is in \(X\).

Aangezien er in \(Y\) een open verzameling bestaat waarvan het inverse beeld niet open is in \(X\), is de afbeelding \(g\) niet continu.

Opmerking: Samengevat is een afbeelding continu als het inverse beeld van elke open verzameling in de doelruimte (\(Y\)) open is in het domein (\(X\)). In het eerste voorbeeld is de functie \(f\) continu omdat aan deze voorwaarde altijd wordt voldaan. De functie \(g\) is dat niet, omdat zij deze eigenschap niet voor alle open verzamelingen heeft.

Definitie van een homeomorfisme

Laat \( X \) en \( Y \) twee topologische ruimten zijn, en \( f : X \to Y \) een bijectieve afbeelding met inverse \( f^{-1} : Y \to X \). Als zowel \( f \) als \( f^{-1} \) continu zijn, dan heet \( f \) een homeomorfisme en zijn de ruimten \( X \) en \( Y \) homeomorf, oftewel \( X \cong Y \).

Deze ruimten worden ook wel topologisch equivalent genoemd.

Wat betekent dat concreet?

Twee ruimten zijn homeomorf, of topologisch equivalent, wanneer ze dezelfde fundamentele structuur delen vanuit topologisch oogpunt, ook al verschillen hun geometrische vormen aanzienlijk.

Een homeomorfisme wordt gekarakteriseerd door drie basisvoorwaarden:

1. Bijectiviteit: De afbeelding \( f : X \to Y \) is zowel injectief als surjectief. Elk punt van \( X \) komt overeen met precies één punt van \( Y\), en omgekeerd.
2. Continuïteit van \( f \): De afbeelding is continu wanneer het inverse beeld van elke open verzameling in \( Y\) open is in \( X\).
3. Continuïteit van \( f^{-1} \): De inverse \( f^{-1} : Y \to X \) moet eveneens continu zijn, wat betekent dat het inverse beeld van elke open verzameling in \( X\) open is in \( Y\).

Voorbeeld: Stel je een vel papier voor dat wordt opgerold tot een cilinder. De cilinder en het vlakke vel zijn homeomorf omdat je van de ene naar de andere kunt overgaan zonder te snijden of te lijmen - eenvoudig door op te rollen of uit te rollen. Hoewel hun geometrische vormen verschillen, blijft hun topologische structuur (de open verzamelingen) gelijk.

Het is belangrijk om te benadrukken dat een bijectieve, continue afbeelding \( f \) niet noodzakelijk een continue inverse \( f^{-1} \) heeft, tenzij \( f \) bovendien een open afbeelding is.

Met andere woorden: een continue en bijectieve functie is niet per se een homeomorfisme als haar inverse niet continu is.

In de topologie noemt men een afbeelding \( f : X \to Y \) continu wanneer het inverse beeld van elke open verzameling in \( Y\) open is in \( X\).

Dat betekent echter niet dat het directe beeld van een open verzameling in \( X\) noodzakelijk open is in \( Y\).

Om te waarborgen dat \( f^{-1} \) continu is, moet \( f \) dus niet alleen continu en bijectief zijn, maar ook een open afbeelding.

Voorbeeld

Beschouw de volgende topologische ruimten:

• \( X = (a, b) \) met de topologie \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
• \( Y = (1, 2) \) met de topologie \( T_Y = \{\emptyset, Y\} \).

We definiëren een afbeelding \( f : X \to Y \) door \( f(a) = 1 \) en \( f(b) = 2 \).

Deze afbeelding is duidelijk bijectief: elk element van \( X \) correspondeert met precies één element van \( Y \), en omgekeerd.

Opmerking: In het schema worden de open verzamelingen weergegeven door cirkels. In \( X \) zijn \{a\}, \{b\} en \{a, b\} open; in \( Y \) is alleen \{1, 2\} open. De lege verzameling, die per definitie open is, wordt hier niet weergegeven.

We onderzoeken nu de continuïteit van \( f \) en van haar inverse \( f^{-1} \).

• Continuïteit van \( f \)
  De topologie \( T_Y \) bevat slechts \( \emptyset \) en \( Y \). We krijgen:
  • \( f^{-1}(\emptyset) = \emptyset \), dat open is in \( T_X \)
  • \( f^{-1}(Y) = X \), eveneens open in \( T_X \)
  Dus \( f \) is continu.
• Continuïteit van \( f^{-1} \)
  We beschouwen nu \( f^{-1} : Y \to X \), met \( f^{-1}(1) = a \) en \( f^{-1}(2) = b \). Voor de open verzamelingen van \( X \) geldt:
  • \( f^{-1}(\emptyset) = \emptyset \), open in \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), dat niet open is in \( T_Y \)
  • \( f^{-1}(\{b\}) = \{2\} \), evenmin open in \( T_Y \)
  • \( f^{-1}(X) = Y \), open in \( T_Y \)
  Omdat sommige inverse beelden niet open zijn, is \( f^{-1} \) niet continu.

We besluiten dat hoewel \( f \) bijectief en continu is, haar inverse dat niet is. \( f \) is dus geen homeomorfisme.

Dit voorbeeld laat zien dat bijectiviteit en continuïteit van een afbeelding niet voldoende zijn om te garanderen dat haar inverse ook continu is.

Opmerking: Het ontbreken van continuïteit van \( f^{-1} \) komt voort uit het verschil tussen de topologieën: de topologie van \( X \) is fijner (rijker aan open verzamelingen) dan die van \( Y \), die grover is.

Voorbeeld 2

We bekijken nu een ander voorbeeld met verschillend gekozen topologieën:

• \( X = (a, b) \) met \( T_X = \{\emptyset, \{a\}, X\} \).
• \( Y = (1, 2) \) met \( T_Y = \{\emptyset, \{1\}, Y\} \).

We definiëren \( f : X \to Y \) door \( f(a) = 1 \) en \( f(b) = 2 \).

Ook in dit geval is \( f \) bijectief.

Laten we nagaan of \( f \) en \( f^{-1} \) continu zijn.

• Continuïteit van \( f \)
  De open verzamelingen van \( Y \) zijn \( \emptyset \), \(\{1\}\) en \( Y \):
  • \( f^{-1}(\emptyset) = \emptyset \), open in \( T_X \)
  • \( f^{-1}(\{1\}) = \{a\} \), open in \( T_X \)
  • \( f^{-1}(Y) = X \), open in \( T_X \)
  Alle inverse beelden zijn open, dus \( f \) is continu.
• Continuïteit van \( f^{-1} \)
  De open verzamelingen van \( X \) zijn \( \emptyset \), \(\{a\}\) en \( X \):
  • \( f^{-1}(\emptyset) = \emptyset \), open in \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), open in \( T_Y \)
  • \( f^{-1}(X) = Y \), eveneens open in \( T_Y \)
  De inverse \( f^{-1} \) is dus ook continu.

We concluderen dat \( f \) bijectief en continu is, en dat haar inverse dat eveneens is. Daarom is \( f \) een homeomorfisme.

Het verschil met het eerste voorbeeld ligt in het gekozen paar topologieën, die hier beter op elkaar zijn afgestemd.

Opmerking: Dit voorbeeld illustreert dat, om de continuïteit van de inverse en dus het bestaan van een homeomorfisme te waarborgen, de topologieën van \( X \) en \( Y \) onderling compatibel moeten zijn.

Verschil tussen homeomorfismen en andere topologische transformaties

Hoewel de term “homeomorfisme” soms in brede zin wordt gebruikt om topologische transformaties aan te duiden, verwijst hij in strikte zin naar een specifieke categorie binnen deze groep.

Homeomorfismen en topologische transformaties zijn nauw verwant, maar drukken niet exact hetzelfde begrip uit:

• Topologische transformaties
  Dit is een algemene term voor afbeeldingen tussen topologische ruimten die fundamentele eigenschappen behouden, zoals continuïteit, samenhang en compactheid. Deze categorie omvat de homeomorfismen, maar ook andere belangrijke typen transformaties, zoals isotopieën, homotopieën en diffeomorfismen.
• Homeomorfismen
  Dit zijn bijectieve, continue afbeeldingen waarvan ook de inverse continu is. Ze leggen een een-op-eenrelatie vast tussen twee ruimten en behouden volledig hun topologische structuur. Twee ruimten die door een homeomorfisme met elkaar verbonden zijn, zijn topologisch niet van elkaar te onderscheiden, ook al kunnen hun geometrische vormen sterk verschillen.

Samenvattend: elk homeomorfisme is een topologische transformatie, maar niet elke topologische transformatie is een homeomorfisme. Sommige afbeeldingen behouden wel belangrijke topologische eigenschappen, maar voldoen niet aan de strengere voorwaarden die een homeomorfisme definiëren.

Aanvullende opmerkingen

Enkele nuttige verduidelijkingen om het begrip en de betekenis van homeomorfismen beter te begrijpen:

• Topologische eigenschap
  Een topologische eigenschap is een intrinsiek kenmerk van een ruimte dat onveranderd blijft onder homeomorfismen. Met andere woorden, als twee ruimten homeomorf zijn (verbonden door een bijectieve, continue afbeelding met een continue inverse), dan delen ze exact dezelfde topologische eigenschappen.
• De stelling van Hausdorff over homeomorfismen
  Deze stelling stelt dat als \( f : X \to Y \) een homeomorfisme is en \( X \) een Hausdorff-ruimte is, dan is \( Y \) dat ook. Met andere woorden, omdat homeomorfismen topologische eigenschappen behouden, wordt de eigenschap van puntenscheiding die kenmerkend is voor Hausdorff-ruimten overgedragen van \( X \) naar \( Y \).
• Het algebraïsche equivalent van een homeomorfisme is een groepsisomorfisme. Waar een isomorfisme de algebraïsche structuur van een object bewaart, bewaart een homeomorfisme de topologische structuur, dat wil zeggen de organisatie van open verzamelingen binnen een ruimte.

Enzovoort.