Topologische onderruimte
Een topologische onderruimte ontstaat wanneer we een deelverzameling van een topologische ruimte bekijken en haar de topologie geven die rechtstreeks wordt afgeleid van de grotere ruimte. Dit maakt het mogelijk om eigenschappen zoals openheid en geslotenheid op een consistente manier binnen de kleinere ruimte te onderzoeken.
Zij \( (X, T) \) een topologische ruimte, waarbij \( X \) de verzameling is en \( T \) de familie van open verzamelingen. Voor een deelverzameling \( Y \subseteq X \) definiëren we de geïnduceerde topologie als: \[ T_Y = \{ U \cap Y \mid U \in T \} \] Deze topologie bevat precies alle snijpunten van open verzamelingen uit \( X \) met de deelverzameling \( Y \).
Een verzameling \( V \subseteq Y \) is dus open in de geïnduceerde topologie wanneer ze ontstaat als het snijpunt van een open verzameling uit \( X \) met \( Y \).
Dit geeft meteen een helder beeld van wat de open verzamelingen in \( Y \) zijn:
$$ V_{open \ in \ Y} = U \cap Y $$
Op dezelfde manier zijn de gesloten verzamelingen in de onderruimte precies die van de vorm:
$$ V_{closed \ in \ Y} = C \cap Y $$
Opmerking: Een verzameling kan open zijn in \( Y \) zonder open te zijn in \( X \). Ook komen verzamelingen voor die tegelijk open én gesloten zijn, de zogenoemde clopen verzamelingen.
Voorbeeld: de onderruimte [0, 1]
Beschouw \( \mathbb{R} \) met de standaardtopologie, waar open intervallen de basis vormen. Neem nu \( Y = [0, 1] \) als onderruimte. De open verzamelingen in deze onderruimte worden gevormd door alle snijpunten van open intervallen met dit gesloten interval.
Een eenvoudig voorbeeld is het interval (-1, 0.5), dat open is in \( \mathbb{R} \). Het snijpunt met \( Y \) vormt een open verzameling in de onderruimtetopologie:
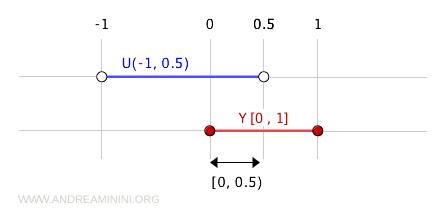
$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$
Dit interval is niet open in \( \mathbb{R} \), maar wel in de onderruimte \( Y \). Het omgekeerde kan ook: een verzameling als \( [0, 0.5] \) is gesloten in de onderruimtetopologie omdat het het snijpunt is van een gesloten interval uit \( \mathbb{R} \) met \( Y \):
$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$
Opmerking: Verzamelingen zoals [0,a) of (a,1], met \( 0 < a < 1 \), zijn typische voorbeelden die niet open zijn in \( \mathbb{R} \), maar wél open worden in \( Y = [0,1] \) door snijpuntvorming.
Daarnaast bestaan er verzamelingen die zowel in \( X \) als in \( Y \) open of gesloten zijn. Zo zijn \( (0.2, 0.8) \) en \( [0.2, 0.8] \) respectievelijk open en gesloten in beide topologieën.
Interessant is dat \( [0, 1] \) in de onderruimtetopologie zowel open als gesloten is. In deze context noemen we zo'n verzameling clopen.
- Waarom open?
Omdat het snijpunt van \( Y \) met een open verzameling van \( \mathbb{R} \) opnieuw \( Y \) oplevert: $$ \mathbb{R} \cap [0,1] = [0,1] $$ - Waarom gesloten?
Omdat het snijpunt van \( [0,1] \) met zichzelf opnieuw \( [0,1] \) is, en het complement binnen \( Y \) leeg is, wat altijd open is.
Dit illustreert hoe de topologie op een onderruimte een eigen karakter kan krijgen, hoewel zij volledig bepaald blijft door de topologie van de oorspronkelijke ruimte.
Voorbeeld 2: de gehele getallen als onderruimte
De verzameling \( \mathbb{Z} \) vormt een topologische onderruimte van \( \mathbb{R} \) met de standaardtopologie. Elk geheel getal kan worden geselecteerd als snijpunt van een open interval met \( \mathbb{Z} \). Bijvoorbeeld:
$$ (6.5,7.5) \cap \mathbb{Z} = \{7\} $$
Dit toont aan dat ieder singleton van een geheel getal open is in de geïnduceerde topologie. Meer nog: elke deelverzameling van \( \mathbb{Z} \) is open, omdat ze altijd als snijpunt met een geschikt interval kan worden geschreven.
Voorbeeld:
$$ (5.5,8.5) \cap \mathbb{Z} = \{6,7,8\} $$
De geïnduceerde topologie op \( \mathbb{Z} \) valt hierdoor samen met de discrete topologie.
Opmerking: De discrete topologie op \( \mathbb{Z} \) is geen deelruimtetopologie van \( \mathbb{R} \). Het is een zelfstandige topologie, maar zij komt exact overeen met de topologie die \( \mathbb{R} \) op \( \mathbb{Z} \) induceert.
Voorbeeld 3
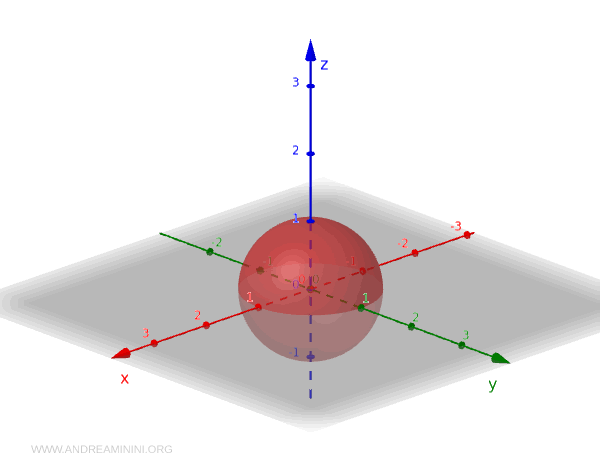
Bekijk de driedimensionale euclidische ruimte \( \mathbb{R}^3 \) met de standaardtopologie, waarin open verzamelingen worden opgebouwd uit unies van open bollen. Binnen deze ruimte speelt de eenheidsfeer \( S^2 \) een centrale rol. Dit is het oppervlak gevormd door alle punten op afstand 1 van de oorsprong:
$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$
Wanneer we \( S^2 \) als topologische onderruimte bekijken, ontstaat de bijbehorende topologie door simpelweg de open verzamelingen van \( \mathbb{R}^3 \) te beperken tot de sfeer:
$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ open is in } \mathbb{R}^3 \} $$
Een verzameling \( V \subseteq S^2 \) is dus open zodra zij kan worden beschreven als het snijpunt van de sfeer met een open verzameling in de omringende ruimte. In de praktijk levert dat een intuïtieve manier op om open gebieden op de sfeer te herkennen.
Hier volgen enkele voorbeelden die duidelijk maken hoe de onderruimtetopologie op \( S^2 \) werkt:
- Een open omgeving die de hele sfeer omvat
Neem het open gebied $$ U = \{ (x,y,z) \mid x^2+y^2+z^2 < 2 \} $$ Dit bevat de hele sfeer, zodat $$ U \cap S^2 = S^2 $$ De sfeer zelf is dus open in haar eigen onderruimtetopologie. - Een open regio op de sfeer
Beschouw het bovenste halfrond: $$ U = \{ (x,y,z) \mid x^2+y^2+z^2 = 1 \text{ en } z > 0 \} $$ Het snijpunt met \( S^2 \) geeft het open gebied $$ \{ (x,y,z) \in S^2 \mid z > 0 \} $$ Dit is een typisch voorbeeld van een open deelverzameling op de sfeer. - Structuur van de topologie op \( S^2 \)
Zoals altijd in een topologische ruimte zijn \( \emptyset \) en \( S^2 \) zelf open.- De doorsnede van een eindig aantal open verzamelingen op de sfeer blijft open.
- Elke unie van open verzamelingen, hoe groot ook, blijft open.
De boodschap is simpel: de topologie van \( S^2 \) wordt volledig bepaald door die van \( \mathbb{R}^3 \). Elk open gebied op de sfeer is het snijpunt met een open gebied in de driedimensionale ruimte.
Belangrijke eigenschappen van de onderruimtetopologie
De onderruimtetopologie heeft een aantal structurele kenmerken die altijd gelden wanneer we een deelverzameling \( Y \subseteq X \) als zelfstandige topologische ruimte bekijken:
- Open verzamelingen
Een verzameling is open in \( Y \) wanneer zij kan worden geschreven als \( U \cap Y \), met \( U \) open in \( X \). - Basisopen verzamelingen
Standaard zijn zowel \( \emptyset \) als de hele verzameling \( Y \) open:
- \( \emptyset = \emptyset \cap Y \)
- \( Y = X \cap Y \) - Eindige doorsneden blijven open
Neem open verzamelingen \( V_i = U_i \cap Y \). Dan geldt: $$ V_1 \cap \cdots \cap V_n = (U_1 \cap \cdots \cap U_n) \cap Y $$ hetgeen opnieuw een open verzameling in \( Y \) oplevert. - Willekeurige unies blijven open
Unies van open verzamelingen in \( Y \) blijven open, hoe groot of complex de indexverzameling ook is: $$ \bigcup_{\alpha \in I} V_\alpha = \left( \bigcup_{\alpha \in I} U_\alpha \right) \cap Y $$
Opmerkingen en verdere inzichten
Bij het werken met onderruimten zijn enkele observaties bijzonder nuttig:
- Voor elke deelverzameling \( Y \subseteq \mathbb{R}^n \) valt de standaardtopologie samen met de onderruimtetopologie die door \( \mathbb{R}^n \) wordt geïnduceerd.
Voorbeeld: Neem \( Y = [-1,0) \cup (0,1] \subseteq \mathbb{R} \). De intervallen \( [-1,0) \) en \( (0,1] \) zijn open in de standaardtopologie van \( Y \) omdat ze snijpunten zijn van \( Y \) met open intervallen in \( \mathbb{R} \): $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ De beide topologieën vallen hiermee volledig samen. Bovendien zijn deze verzamelingen in \( Y \) ook gesloten, zodat ze clopen zijn.
- Basistheorema voor onderruimten
Als \( B_X \) een basis is voor de topologie van \( X \), dan vormt $$ B_Y = \{ B \cap Y \mid B \in B_X \} $$ een basis voor de topologie die \( X \) op \( Y \) induceert.
Deze eigenschappen vormen het fundament voor het analyseren van topologische onderruimten en maken duidelijk hoe structuren uit de grotere ruimte doorwerken in haar deelverzamelingen.