Clopen verzamelingen

Een verzameling heet clopen wanneer zij in een gegeven topologie tegelijkertijd open en gesloten is.

Dat klinkt op het eerste gezicht als een tegenspraak, want in de bekende wereld van de reële getallen zijn open en gesloten verzamelingen meestal elkaars tegenpolen. In de topologie is het echter heel goed mogelijk dat één en dezelfde verzameling aan beide definities voldoet.

Het woord clopen komt van de samentrekking van de Engelse termen closed en open. Clopen verzamelingen nemen dus een bijzondere positie in, omdat zij de eigenschappen van open verzamelingen en gesloten verzamelingen combineren.

Een verzameling is clopen wanneer zij én open is én haar complement in dezelfde topologie ook open is.

Opmerking: In de gebruikelijke topologie op de reële getallen zijn clopen verzamelingen zeldzaam. In andere topologische ruimten kunnen zij echter veel vaker voorkomen en inzicht geven in de opbouw en structuur van die ruimten.

Een concreet voorbeeld
De lege verzameling en de volledige verzameling zijn altijd clopen

Een concreet voorbeeld

Beschouw de verzameling $X=\{a,b,c,d\}$, uitgerust met een topologie $T$.

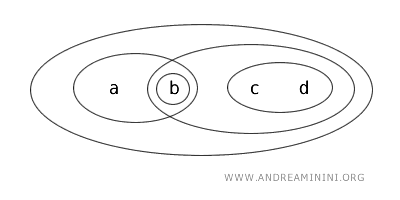
Visueel voorbeeld van een clopen verzameling

In deze topologie $T$ zijn de volgende verzamelingen open: $\{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, \{a,b,c,d\}, \varnothing$.

Daaruit volgt dat $\{a,b\}$ een open verzameling is in $T$.

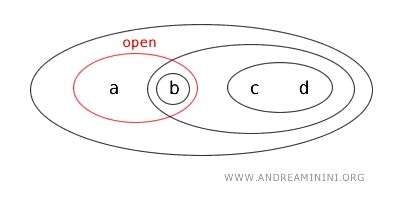
Deelverzameling {a,b} voorgesteld als open verzameling

Daarnaast is $\{a,b\}$ ook het complement van de open verzameling $\{c,d\}$:

$$ X - \{ c,d \} = \{a , b \} $$

Omdat het complement van een open verzameling altijd een gesloten verzameling is, volgt dat $\{a,b\}$ eveneens gesloten is.

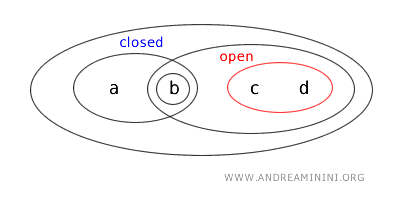
Deelverzameling {a,b} voorgesteld als gesloten verzameling

We zien dus dat $\{a,b\}$ tegelijk open en gesloten is in $T$. Het is daarmee een voorbeeld van een clopen verzameling.

De lege verzameling en de volledige verzameling zijn altijd clopen

In elke topologie op een verzameling $X$ zijn de volledige verzameling $X$ en de lege verzameling $\varnothing$ noodzakelijkerwijs clopen.

Volgens de axioma’s van de topologie zijn zowel $\varnothing$ als $X$ altijd open. Een verzameling is gesloten wanneer haar complement open is, en daarmee zijn beide automatisch ook gesloten.

De lege verzameling ($\varnothing$)
Zij is open volgens de definitie. Haar complement $X$ is open en daardoor is $\varnothing$ ook gesloten. De lege verzameling is dus clopen.
De volledige verzameling ($X$)
Zij is open volgens de definitie. Haar complement $\varnothing$ is open en daardoor is $X$ eveneens gesloten. Ook $X$ is dus clopen.

Hieruit volgt dat in elke topologie altijd minstens twee clopen verzamelingen bestaan: $\varnothing$ en $X$. Andere clopen verzamelingen, zoals in het eerdere voorbeeld, geven vaak waardevolle informatie over de structuur van de ruimte waarin zij voorkomen.

Enzovoort.