Open bal

In de topologie verwijst een open bal naar de verzameling van alle punten die binnen een bepaalde afstand liggen van een vast punt, het centrum $ c $. Concreet bestaat de open bal uit alle punten waarvan de afstand tot $ c $ kleiner is dan een straal $ r $: $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

Dit idee speelt een centrale rol in metrische ruimtes $ M $. De functie $ d $, de metriek, bepaalt hoe afstanden tussen punten worden gemeten. Door deze afstandsfunctie krijgt de ruimte structuur en kunnen we nauwkeurig beschrijven wat het betekent dat punten dichter of verder van elkaar liggen.

Een open bal wordt volledig bepaald door twee gegevens, het centrum en de straal. Die eenvoud maakt haar tot een krachtig hulpmiddel in de wiskundige analyse.

Het woord « open » heeft hier een precieze betekenis. Elk punt dat binnen de open bal ligt, kan zelf dienen als centrum van een kleinere open bal die helemaal in de oorspronkelijke bal past. Dit lokale perspectief is kenmerkend voor de topologie.

Opmerking: Open ballen blijven onveranderd onder verschuivingen of schaalvergroting. Dat betekent dat hun topologische eigenschappen niet afhangen van waar ze liggen of hoe groot ze zijn.

Neem als voorbeeld het vlak $ \mathbb{R}^2 $. De afstand tussen een punt $ p = (x, y) $ en een centrum $ c = (x_0, y_0) $ wordt berekend met de vertrouwde Euclidische formule:

$$ d(p,c) = \sqrt{(x - x_0)^2 + (y - y_0)^2} $$

Met deze metriek vormen open ballen de bouwstenen van de standaardtopologie van het vlak. Ze geven precies aan welke punten als « dicht bij elkaar » worden beschouwd.

De volledige topologie wordt gegenereerd door alle mogelijke open ballen:

$$ B = \{ B(p, r) \mid p \in \mathbb{R}^2,\ r > 0 \} $$

Hierin staat $ p $ voor een willekeurig punt van het vlak en $ r $ voor een positieve straal.

visuele voorstelling van open ballen in de standaardtopologie op R^2

Onder de vele mogelijke manieren om een topologie op $ \mathbb{R}^2 $ te definiëren, is die van de Euclidische open ballen de meest gebruikte. Ze sluit nauw aan bij onze intuïtie over afstand en nabijheid.

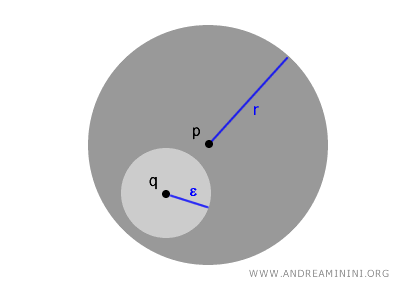
Bovendien geldt in elke open bal $ B(p,r) $ dat elk punt $ q $ opnieuw het middelpunt kan zijn van een kleinere open bal $ B(q, \epsilon) $ die geheel binnen $ B(p,r) $ ligt. Zo ontstaat een verfijnde, steeds verder inzoomende structuur.

Dit wordt formeel weergegeven als:

$$ \forall\ q \in B(p,r),\ \exists\ \epsilon > 0\ \text{zodat}\ B(q,\epsilon) \subset B(p,r) $$

grafische illustratie van een kleinere open bal binnen een grotere open bal

Door dit proces telkens opnieuw te herhalen ontstaat een helder beeld van hoe topologische ruimtes lokaal zijn opgebouwd. De open bal fungeert daarbij als een van de meest fundamentele en inzichtelijke structuren.