Gesloten verzamelingen

Een deelverzameling $ B $ van een topologische ruimte $ X $ heet gesloten wanneer voor elk punt in het complement $ u \in X - B $ een omgeving bestaat die volledig binnen dit complement $ X - B $ ligt.
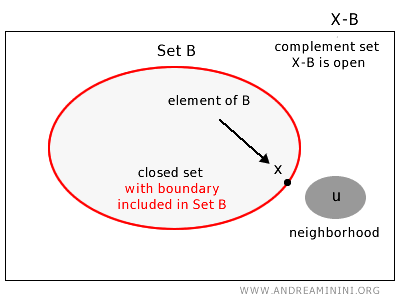
voorbeeld van een gesloten verzameling

Met andere woorden, een verzameling is gesloten wanneer zij al haar grenspunten bevat.

Nauwkeuriger geformuleerd is een verzameling $ B $ in een topologische ruimte $ X $ gesloten wanneer het complement $ X - B $ een open verzameling vormt.

Opmerking : Dit houdt in dat er in $ B $ ten minste één punt voorkomt waarvoor geen enkele omgeving volledig in $ B $ kan worden opgenomen.

Een concreet voorbeeld
Het complement van een gesloten verzameling
Voorbeeld
Eigenschappen van gesloten verzamelingen
Voorbeeld
Aanvullende opmerkingen

Een concreet voorbeeld

Beschouwen we de reële lijn $ \mathbb{R} $ en een gesloten interval.

Wat is een gesloten interval? Een gesloten interval in $ \mathbb{R} $ bestaat uit alle punten $ x $ waarvoor $ a \leq x \leq b $, met $ a $ en $ b $ reële getallen en $ a < b $. Beide eindpunten behoren tot de verzameling.

Zo'n interval noteren we als $[a,b]$. De rechte haken geven aan dat zowel $ a $ als $ b $ inbegrepen zijn.

Een eenvoudig voorbeeld is het gesloten interval $[3,10]$, dat een gesloten deelverzameling vormt van de reële lijn $ \mathbb{R} $.

In dit geval bestaat de verzameling $ B $ uit alle reële getallen tussen 3 en 10, inclusief de uiteinden.

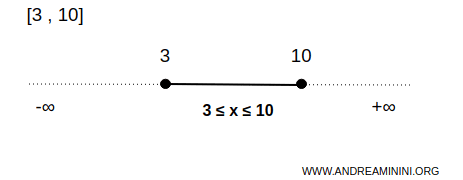
visueel voorbeeld van een gesloten verzameling

Met andere woorden, elk punt $ x $ waarvoor $ 3 \leq x \leq 10 $ geldt, behoort tot $ B $, inclusief de grenspunten $ x=3 $ en $ x=10 $.

Dit betekent echter niet dat ieder punt een omgeving heeft die volledig binnen $[3,10]$ blijft.

Elke omgeving rond $ x=3 $ zal bijvoorbeeld ook waarden bevatten die kleiner zijn dan 3 en dus buiten het interval liggen.

Opmerking : Zelfs wanneer we een extreem kleine omgeving nemen, zoals $ 3 \pm 0{,}00000001 $, dan ligt $ 3 - 0{,}00000001 $ nog steeds buiten $[3,10]$. Voor het bovenste grenspunt $ x=10 $ geldt dezelfde redenering: geen enkele omgeving past volledig binnen het interval.

Dit is een klassiek voorbeeld van een gesloten verzameling in één dimensie.

Andere voorbeelden van gesloten verzamelingen

We kunnen dit idee uitbreiden naar het vlak ($\mathbb{R}^2$).

Neem bijvoorbeeld de verzameling punten binnen een schijf met straal $ r=1 $ en middelpunt $(0,0)$:

$$ x^2 + y^2 \leq 1 $$

Deze ongelijkheid beschrijft alle punten waarvan de afstand tot $(0,0)$ hoogstens 1 bedraagt. Zowel het inwendige van de schijf als de omtrek maken deel uit van de verzameling.

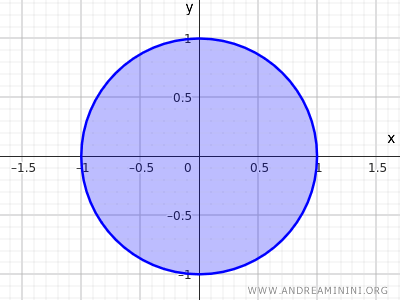
gesloten verzameling in het vlak

Dit vormt opnieuw een gesloten verzameling.

De punten op de cirkel $ x^2 + y^2 = 1 $ hebben echter geen enkele omgeving die volledig in de gesloten schijf kan worden opgenomen.

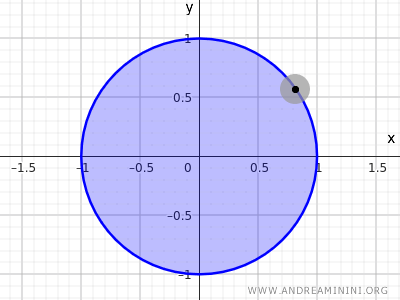
gesloten verzameling geïllustreerd

Opmerking : In topologie geldt dat de cirkel $ x^2 + y^2 = 1 $ op zichzelf noch open noch gesloten is in $ \mathbb{R}^2 $. Zij bevat immers enkel de rand en niet het inwendige. De verzameling $ x^2 + y^2 \leq 1 $, die zowel rand als inwendige omvat, vormt daarentegen een typisch voorbeeld van een gesloten verzameling omdat zij al haar grenspunten bevat.

Op dezelfde manier kunnen we dit doortrekken naar drie dimensies, met een gesloten bol, en zelfs naar het $ n $-dimensionale geval, met een gesloten $ n $-bol.

Het complement van een gesloten verzameling

In een topologische ruimte $ X $ is het complement van een gesloten verzameling $ C $ een open verzameling, genoteerd als $ X - C $.

Met andere woorden, als $ C $ gesloten is in $ X $, dan is het complement $ X - C $ per definitie open.

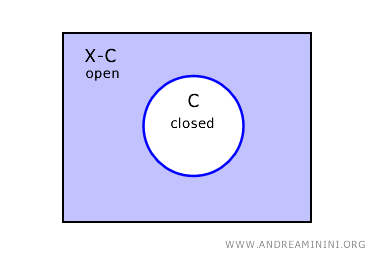
complement van een gesloten verzameling

Het omgekeerde geldt eveneens: als een verzameling $ U $ open is, dan vormt haar complement $ X - U $ een gesloten deelverzameling van $ X $.

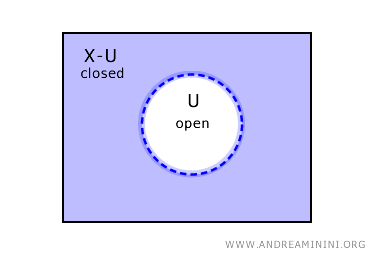
complement van een open verzameling

Dit zijn echter niet de enige mogelijkheden. In bepaalde topologische ruimtes bestaan er verzamelingen die zowel open als gesloten zijn, en ook verzamelingen die noch open noch gesloten zijn.

Daaruit volgt dat een verzameling die niet gesloten is, niet noodzakelijk open hoeft te zijn. Evenmin geldt dat een verzameling die niet open is, per definitie gesloten moet zijn.

Voorbeeld

Beschouwen we een topologische ruimte $ (X, T) $, waarin de verzameling $ X = \{a,b,c,d\} $ uit vier elementen bestaat en de topologie $ T $ wordt bepaald door de volgende open verzamelingen:

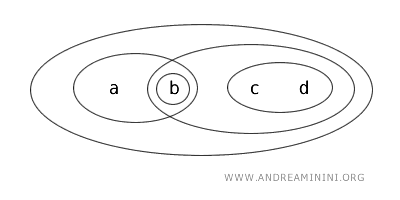
voorbeeld

De open verzamelingen in deze topologie zijn: $ \{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, X $ en de lege verzameling $ \varnothing $.

Laten we enkele specifieke gevallen bekijken:

De verzameling $ \{b\} $ is open, want zij komt expliciet voor in de definitie van de topologie.
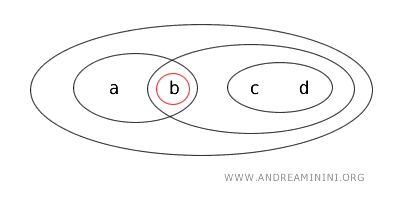
De verzameling $ \{a\} $ is gesloten, omdat het complement een open verzameling is. We hebben namelijk $ X - \{a\} = \{b,c,d\} $, en deze verzameling is open.
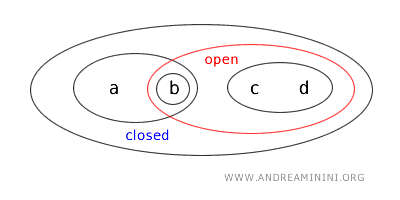
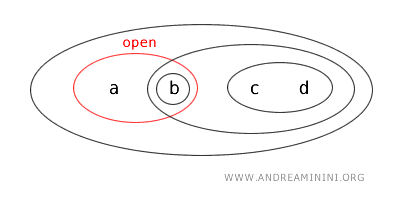
De verzameling $ \{a,b\} $ is zowel open als gesloten (clopen). In de gebruikelijke topologie op $ \mathbb{R} $ is dit uitzonderlijk, maar in meer algemene topologische ruimten is het mogelijk dat een verzameling tegelijk open en gesloten is wanneer ook haar complement open is. Hier is $ \{a,b\} $ open volgens de topologie, en bovendien is het complement $ X - \{a,b\} = \{c,d\} $ eveneens open. Daarom is $ \{a,b\} $ tegelijk een gesloten verzameling.
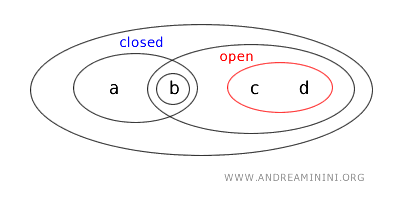
De verzameling $ \{b,c\} $ is noch open noch gesloten. Zij behoort niet tot de open verzamelingen van de topologie, en ook haar complement $ X - \{b,c\} = \{a,d\} $ is niet open. Daardoor voldoet zij aan geen van beide definities.

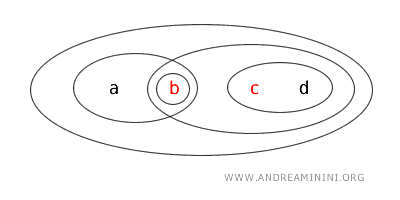
Dit voorbeeld toont duidelijk dat een verzameling in een topologische ruimte open kan zijn, gesloten kan zijn, beide tegelijk (clopen), of geen van beide.

Eigenschappen van gesloten verzamelingen

Een gesloten verzameling wordt gedefinieerd als het complement van een open verzameling. Enkele fundamentele eigenschappen zijn:

De lege verzameling ($\varnothing$) en de volledige ruimte $ X $ zijn altijd gesloten.
De doorsnede van een willekeurige verzameling gesloten verzamelingen, eindig of oneindig, is opnieuw gesloten.
De unie van een eindig aantal gesloten verzamelingen is eveneens een gesloten verzameling.

Voorbeeld

In de gebruikelijke topologie van de Euclidische ruimte $ \mathbb{R}^n $ vormt elk geïsoleerd punt een gesloten verzameling.

Neem een punt $ n $ op de reële as ($ \mathbb{R}^1 $). Het complement bestaat uit alle punten van $ \mathbb{R}^1 $ behalve $ n $.

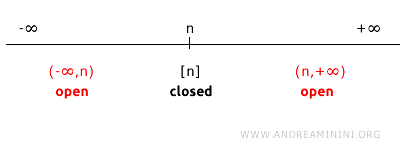
voorbeeld

Het complement van $\{n\}$ is de unie van twee open intervallen: $(-\infty, n) \cup (n, +\infty)$.

Aangezien de intervallen $(-\infty, n)$ en $(n, +\infty)$ open zijn, is hun unie eveneens open.

Daarom is $\{n\}$ een gesloten verzameling: haar complement is open.

Toch geldt dit niet in elke topologie. In sommige topologische ruimten zijn geïsoleerde punten niet per definitie gesloten. Dit hangt volledig af van de gekozen topologie.

Beschouwen we bijvoorbeeld een topologie op $ \mathbb{R} $ die wordt voortgebracht door de open intervallen $ (n, n+1) $ voor elke gehele $ n $. In deze topologie zijn geïsoleerde punten $ n $ geen gesloten verzamelingen, omdat zij niet kunnen worden uitgedrukt als het complement van een open verzameling.
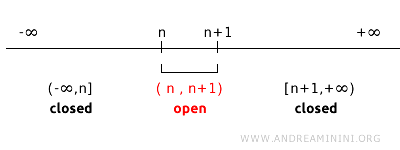
voorbeeld
Zo zijn de verzamelingen $ (1,2) $ en $ (2,3) $ open in deze topologie. Het complement van $ (1,2) $ is $ (-\infty, 1] \cup [2, +\infty) $, terwijl het complement van $ (2,3) $ gelijk is aan $ (-\infty, 2] \cup [3, +\infty) $.

In deze topologie kan er geen open verzameling worden gevonden waarvan het complement precies $\{2\}$ is. In het algemeen heeft elke open verzameling van de vorm $ (n, n+1) $ een complement dat bestaat uit een unie van gesloten intervallen $ (-\infty, n] \cup [n+1, +\infty) $. Daarom zijn geïsoleerde punten $ n $ in deze topologie niet gesloten. Dit onderstreept dat het begrip gesloten verzameling afhankelijk is van de structuur van de gekozen topologie.

Aanvullende opmerkingen

Enkele nuttige observaties:

Gesloten verzamelingen en ophopingspunten
Een ophopingspunt van een verzameling is een punt waarvan elke omgeving, hoe klein ook, steeds minstens één ander punt van die verzameling bevat. Dit is een cruciale eigenschap: een verzameling is gesloten wanneer zij al haar ophopingspunten bevat.

Voorbeeld: Beschouw het gesloten interval $[0,1]$ op de reële as. Deze verzameling bevat al haar ophopingspunten.

Het punt $0{,}5$ in $[0,1]$ heeft bijvoorbeeld elke open omgeving met oneindig veel punten uit het interval. Dit bevestigt dat het een ophopingspunt is.
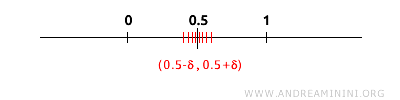
voorbeeld van 0,5 als ophopingspunt

Hetzelfde geldt voor de uiteinden van het interval. Zo is $0$ een ophopingspunt van $[0,1]$, want elke omgeving van $0$ bevat andere punten uit het interval, zoals $0{,}1$, $0{,}01$, $0{,}001$, enzovoort.
ophopingspunten op de uiteinden van [0,1]
Hieruit volgt dat alle punten van $[0,1]$ ophopingspunten zijn.

Een verzameling $ A $ is gesloten dan en slechts dan wanneer $ A = \overline{A} $
In een topologische ruimte is een verzameling $ A $ gesloten wanneer zij samenvalt met haar afsluiting, dat wil zeggen $ A = \overline{A} $. De afsluiting $ \overline{A} $ bevat alle punten van $ A $ samen met haar ophopingspunten. Zodra een verzameling al haar ophopingspunten bevat, is zij per definitie gesloten.

En zo verder.