De unie van de inwendigen van twee verzamelingen
Wanneer we de inwendigen van twee verzamelingen \( A \) en \( B \) samenvoegen, ontstaat er altijd een verzameling die volledig binnen het inwendige van hun unie ligt: \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] Toch betekent dit niet dat beide verzamelingen noodzakelijk samenvallen.
Het inwendige van de unie is dus minstens zo groot als wat we krijgen door de afzonderlijke inwendigen te combineren.
Toch is het vaak niet zo dat:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
De inclusie kan duidelijk strikt zijn:
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
Dit onderscheid helpt ons begrijpen hoe topologische structuren reageren wanneer verzamelingen elkaar raken of overlappen.
Een eerste verkennend voorbeeld
Neem twee open intervallen in \(\mathbb{R}\):
$$ A = (0, 2) \qquad B = (1, 3) $$
Omdat open intervallen samenvallen met hun inwendige, geldt:
$$ \text{Int}(A) = (0, 2) \qquad \text{Int}(B) = (1, 3) $$
Ze samenvoegen geeft:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 3) $$
En voor de unie zelf geldt eveneens:
$$ A \cup B = (0, 3) $$
Het inwendige van de unie is dan:
$$ \text{Int}(A \cup B) = (0, 3) $$
In dit geval vallen beide zijden samen.
Beschouwen we nu gesloten intervallen: $$ A = [0, 2] \qquad B = [2, 3] $$ Hun inwendigen zijn: $$ \text{Int}(A) = (0, 2) \qquad \text{Int}(B) = (2, 3) $$ De unie is \( A \cup B = [0, 3] \), en het inwendige daarvan is: $$ \text{Int}(A \cup B) = (0, 3) $$ De inclusie blijft verschijnen: $$ (0, 2) \cup (2, 3) \subseteq (0, 3) $$ Maar gelijkheid treedt niet op. Het punt \( 2 \) behoort wél tot het inwendige van de unie: $$ 2 \in (0, 3) $$ maar tot geen van de afzonderlijke inwendigen: $$ 2 \not\in (0, 2), \quad 2 \not\in (2, 3) $$ Daardoor volgt vanzelf: $$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$ Dit voorbeeld laat zien hoe grenspunten het verschil kunnen maken.
Voorbeeld 2
Neem opnieuw twee open intervallen, maar nu volledig gescheiden:
$$ A = (0, 1) \qquad B = (2, 3) $$
Hun inwendigen veranderen niet:
$$ \text{Int}(A) = (0, 1) \qquad \text{Int}(B) = (2, 3) $$
En dus:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
Aangezien de unie van open intervallen open blijft, geldt:
$$ \text{Int}(A \cup B) = (0, 1) \cup (2, 3) $$
In dit geval treedt opnieuw gelijkheid op.
Deze voorbeelden illustreren dat de inclusie altijd geldig blijft, maar dat gelijkheid enkel optreedt wanneer er geen subtiele grensovergangen plaatsvinden.
Voorbeeld 3
Ga nu naar het vlak \(\mathbb{R}^2\) en neem twee overlappende open schijven met middelpunten in \( (0, 0) \) en \( (0{,}5, 0) \), beide met straal \( 1 \):
$$ A = \{ (x, y) \mid x^2 + y^2 < 1 \} $$
$$ B = \{ (x, y) \mid (x - 0{,}5)^2 + y^2 < 1 \} $$
Omdat open schijven samenvallen met hun inwendige, blijft:
$$ \text{Int}(A) = A \qquad \text{Int}(B) = B $$
De unie van de inwendigen is dus:
$$ A \cup B $$
Hier ontstaat een gebied waarin de twee schijven gedeeltelijk overlappen.
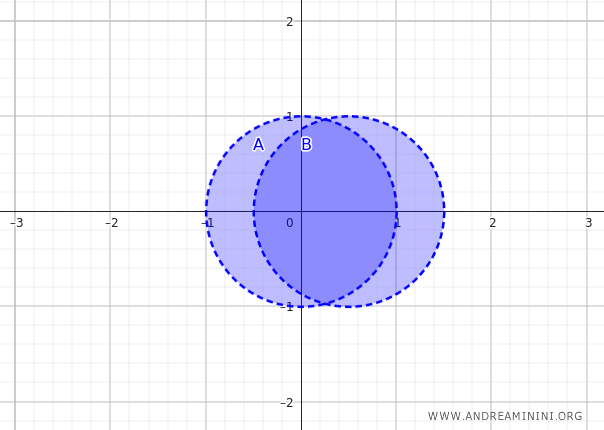
Het inwendige van de unie omvat alle punten waarvoor een volledige open omgeving binnen \( A \cup B \) ligt:
$$ \text{Int}(A \cup B) = A \cup B $$
Ook hier blijft de inclusie geldig:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Waarom deze eigenschap altijd werkt
De reden dat de inclusie altijd geldt, volgt rechtstreeks uit de definitie van het inwendige.
Het inwendige van een verzameling \( X \), aangeduid met \( \text{Int}(X) \), bestaat uit alle punten waarvoor een open omgeving volledig binnen \( X \) ligt.
Neem een punt \( x \) in \( \text{Int}(A) \cup \text{Int}(B) \). Het hoort dan bij het inwendige van ten minste één van beide verzamelingen.
- Behoort \( x \) tot \( \text{Int}(A) \), dan ligt er een open omgeving volledig in \( A \).
- Behoort \( x \) tot \( \text{Int}(B) \), dan ligt er een open omgeving volledig in \( B \).
In beide situaties ligt die omgeving automatisch binnen \( A \cup B \). Daardoor behoort \( x \) noodzakelijk tot het inwendige van de unie.
We krijgen dus altijd:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
En daarmee is de redenering compleet.