Separação de um conjunto por abertos

Considere $ A $ como um subconjunto de um espaço topológico $ X $. Uma forma muito eficiente de entender quando esse subconjunto pode ser dividido em duas partes distintas é analisar como ele interage com dois abertos do mesmo espaço, chamados $ U $ e $ V $. Dizemos que esses abertos separam $ A $ quando três condições fundamentais são cumpridas:

$ A $ está contido na união de $ U $ e $ V $ \[ A \subseteq U \cup V \]
Ambos os abertos encontram $ A $ \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
Nenhum ponto de $ A $ pertence aos dois ao mesmo tempo \[ U \cap V \cap A = \varnothing \]

Essas condições garantem uma divisão muito clara: uma parte de $ A $ fica totalmente em $ U $ e a outra totalmente em $ V $. Esse é exatamente o tipo de configuração que, em topologia, chamamos de separação. A ideia é simples e poderosa, pois permite identificar rapidamente quando um conjunto está dividido em duas regiões distintas.

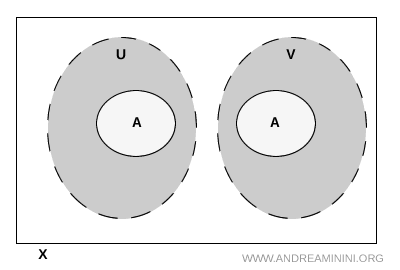
esquema ilustrando a separação de um conjunto por dois abertos

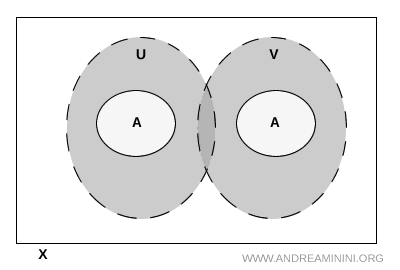
Nota. Mesmo que $ U $ e $ V $ se intersectem fora de $ A $, isso não altera o resultado. Só importa garantir que nenhum ponto de $ A $ esteja nessa interseção externa.
ilustração mostrando que dois abertos podem intersectar-se fora de A sem afetar a separação

Exemplo

Para tornar o conceito mais intuitivo, vamos trabalhar em um dos cenários mais familiares: o espaço $ X = \mathbb{R} $ com a topologia usual. Considere o conjunto:

$$ A = [-2,-1] \cup [1,2] $$

Temos aqui dois intervalos fechados que não se encontram e formam duas partes bem distintas.

Escolhemos agora os seguintes abertos:

$$ U = (-3,0) $$

$$ V = (0,3) $$

Observe a representação gráfica abaixo:

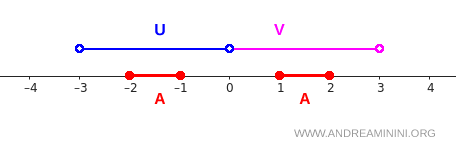
reta real ilustrando U, V e as duas componentes de A

O intervalo $ [-2,-1] $ está completamente dentro de $ U $, enquanto $ [1,2] $ está inteiramente em $ V $. A verificação das condições é direta:

1. O conjunto $ A $ está dentro de $ U \cup V $:

$$ A \subseteq U \cup V $$

2. Ambos os abertos contêm pontos de $ A $:

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

3. Não há ponto de $ A $ que pertença simultaneamente aos dois:

$$ U \cap V \cap A = \varnothing $$

Assim, $ U $ e $ V $ separam o conjunto $ A $ em $ \mathbb{R} $. Como $ A $ já possui duas partes bem definidas, esse exemplo facilita bastante a visualização da ideia de separação, tornando a definição abstrata mais acessível.