Conectividade por interseção não vazia
Sejam \( C_1, C_2, \dots, C_n \subset X \) subconjuntos conexos de um espaço topológico \( X \) tais que a sua interseção não seja vazia: \[
\bigcap_{i=1}^n C_i \neq \varnothing . \] Nessas condições, a união \( \bigcup_{i=1}^n C_i \) também é um conjunto conexo.
Em termos simples, sempre que vários conjuntos conexos compartilham pelo menos um ponto, a sua união continua sendo conexa. A presença desse ponto comum impede que o conjunto resultante possa ser "separado" em partes independentes.
Esse princípio é simples, mas fundamental em topologia, pois permite compreender como a conectividade pode ser preservada mesmo quando diferentes regiões se unem apenas em pontos específicos.
Observação. A condição \( \bigcap_{i=1}^n C_i \neq \varnothing \) é suficiente para garantir a conectividade da união \( \bigcup_{i=1}^n C_i \), mas não é necessária. Uma união de conjuntos conexos pode continuar sendo conexa mesmo sem um ponto comum a todos eles. Isso acontece, por exemplo, quando os conjuntos se sobrepõem de forma progressiva ou se conectam em cadeia.
Um exemplo concreto
Consideremos os seguintes subconjuntos de \( \mathbb{R}^2 \):
- \( C_1 \): o segmento horizontal que liga \( (-1,0) \) a \( (1,0) \)
- \( C_2 \): o segmento vertical que liga \( (0,-1) \) a \( (0,1) \)
- \( C_3 \): o segmento diagonal que liga \( (-1,-1) \) a \( (1,1) \)
Cada um desses conjuntos é conexo.
Além disso, todos eles passam por um mesmo ponto, a saber \( (0,0) \). De fato:
\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]
Portanto, a interseção comum não é vazia:
\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]
De acordo com o critério apresentado, a união desses conjuntos é, portanto, conexa:
\[ C_1 \cup C_2 \cup C_3 \]
Os três segmentos encontram-se em um mesmo ponto central, o que garante a conectividade da união.
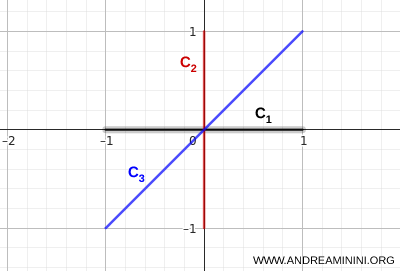
A partir de qualquer ponto de um dos segmentos, é possível alcançar qualquer outro ponto sem sair da união dos conjuntos.
Observação. Existem outros critérios de conectividade que não dependem da existência de um ponto comum a todos os conjuntos. Por exemplo, se os conjuntos \( C_i \) são conexos e se intersectam de forma encadeada, isto é, se \( C_i \cap C_{i+1} \neq \varnothing \), então a união \( \bigcup_i C_i \) é conexa, mesmo que \( \bigcap_i C_i = \varnothing \). Essa condição, porém, não é essencial. A união pode continuar conexa mesmo quando alguns pares consecutivos são disjuntos, desde que outros conjuntos garantam a ligação. Um exemplo clássico é o de três segmentos que formam um triângulo. Embora a interseção global seja vazia, \( \bigcap_i C_i = \varnothing \), a união permanece conexa.
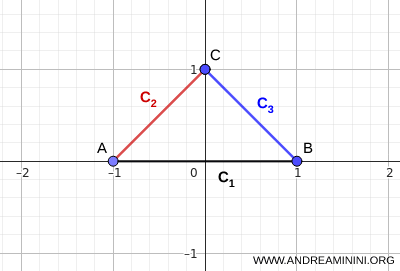
Esse exemplo mostra claramente como a conectividade pode surgir a partir de uma cadeia de interseções locais.
Demonstração
Seja \( X \) um espaço topológico e seja \( \{C_i\}_{i \in I} \) uma família de subconjuntos conexos de \( X \) cuja interseção não é vazia:
\[ \bigcap_{i \in I} C_i \neq \varnothing \]
Suponhamos, por absurdo, que a união
\[ C = \bigcup_{i \in I} C_i \]
não seja conexa.
Nesse caso, existem dois abertos \( U \) e \( V \) que formam uma separação de \( C \), isto é:
- \( U \cap C \neq \varnothing \)
- \( V \cap C \neq \varnothing \)
- \( (U \cap C) \cap (V \cap C) = \varnothing \)
- \( C = (U \cap C) \cup (V \cap C) \)
Como a interseção dos conjuntos \( C_i \) não é vazia, existe um ponto
\[ x \in \bigcap_{i \in I} C_i \]
Esse ponto pertence a todos os conjuntos \( C_i \) e, portanto, pertence a \( C \). Ele deve estar em \( U \) ou em \( V \), mas não em ambos, pois estes formam uma separação de \( C \). Suponhamos, sem perda de generalidade, que
\[ x \in U \quad \text{e} \quad x \notin V \]
Como cada conjunto \( C_i \) está contido em \( C \), temos:
\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]
Os conjuntos \( C_i \cap U \) e \( C_i \cap V \) são abertos na topologia induzida sobre \( C_i \), são disjuntos e a sua união recompõe \( C_i \). Como cada \( C_i \) é conexo, um desses dois conjuntos deve ser necessariamente vazio.
Segue-se que cada \( C_i \) está inteiramente contido em \( U \) ou em \( V \).
Como \( x \in C_i \) e \( x \in U \), é impossível que \( C_i \subset V \). Portanto:
\[ C_i \subset U \quad \text{para todo } i \in I \]
Consequentemente, a união \( C \) também está contida em \( U \):
\[ \bigcup_{i \in I} C_i \subset U \]
Isso contradiz a hipótese de que \( V \cap C \neq \varnothing \).
A contradição mostra que a suposição inicial é falsa. Conclui-se, portanto, que a união \( \bigcup_{i \in I} C_i \) é um conjunto conexo.
E assim se conclui a demonstração.