Topologia

A topologia é um ramo da matemática que estuda as propriedades dos espaços que permanecem inalteradas sob transformações contínuas, como esticar, dobrar ou torcer. Exemplos dessas propriedades incluem conectividade, compacidade e o número de buracos presentes em um objeto.

De forma mais simples, a topologia trata da organização e da conexão entre os espaços, em vez de se preocupar com medidas exatas como distância ou tamanho.

Na topologia, conceitos tradicionais como distância e ângulos deixam de ser relevantes; o foco está na natureza qualitativa das formas e nas possíveis transformações que elas podem sofrer.

O conceito central em topologia é o de espaço topológico, e as transformações fundamentais recebem o nome de homeomorfismos.

Frequentemente descrita como a "geometria da folha de borracha", a topologia enxerga os objetos como se fossem feitos de um material elástico que pode ser esticado ou comprimido, mas não rasgado nem colado. Trata-se de um componente essencial da matemática moderna.

História

O desenvolvimento da topologia começou no século XVIII.

Sua origem remonta ao famoso Problema das Sete Pontes de Königsberg, proposto por Leonhard Euler, que introduziu ideias fundamentais de conectividade e teoria dos grafos.

Esse problema levantou questões cruciais sobre as propriedades dos espaços e lançou as bases da topologia.

O problema das Sete Pontes: Em uma ilha fluvial, havia sete pontes. Partindo de qualquer ponto, seria possível traçar um percurso que atravessasse cada ponte exatamente uma vez? A condição é clara: não se pode atravessar a mesma ponte duas vezes.

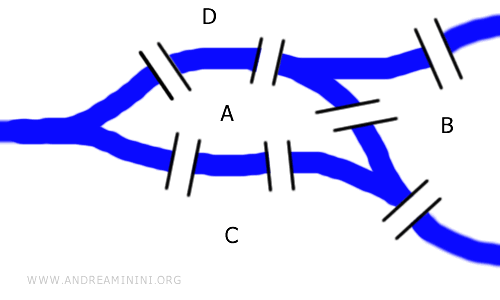
Esse desafio não depende de distâncias nem do comprimento das pontes; é, essencialmente, uma questão topológica que pode ser representada por meio de grafos. O grafo mostrado aqui é topologicamente equivalente ao arranjo original das pontes.

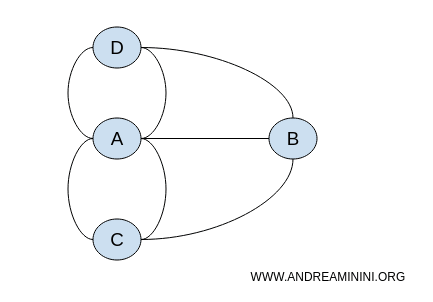
As posições exatas dos nós no grafo são irrelevantes. O que importa são as conexões entre eles. Assim, o problema pode ser descrito por infinitas representações diferentes, todas topologicamente equivalentes.

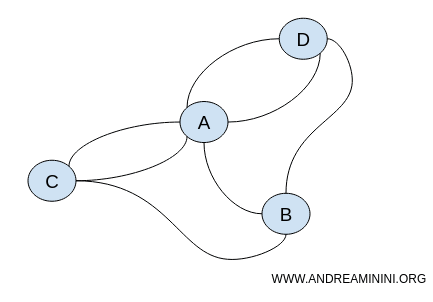
Ambos os grafos preservam as mesmas propriedades topológicas, como continuidade e conectividade.

Euler percebeu que o problema das Sete Pontes de Königsberg, embora geométrico, não envolvia medições de comprimento.

Ele demonstrou que a questão era, na verdade, de natureza posicional e provou que não tinha solução, inaugurando o conceito de "geometria da posição".

Ao longo do século XIX, matemáticos como Carl Friedrich Gauss, August Ferdinand Möbius, Johann Listing, Bernhard Riemann e Felix Klein aprofundaram o estudo das formas e superfícies, consolidando a compreensão das propriedades topológicas.

Nota: Johann Listing cunhou o termo "topologia" em 1847, embora ele só tenha se difundido amplamente na comunidade científica algumas décadas depois.

No século XIX, a geometria da posição encontrou aplicações práticas em áreas como a análise de redes elétricas, com os trabalhos de Gustav Kirchhoff.

Posteriormente, Henri Poincaré, entre o final do século XIX e o início do século XX, deu contribuições decisivas à geometria da posição com suas pesquisas em topologia algébrica.

No século XX, a topologia se desdobrou em especializações como topologia algébrica e topologia geral, com contribuições marcantes de matemáticos como Felix Hausdorff, Georg Cantor e L. E. J. Brouwer, especialmente no campo da matemática abstrata.

Atualmente, a topologia é uma área fundamental da matemática, dedicada ao estudo das propriedades que permanecem invariantes sob transformações contínuas.

A disciplina abrange hoje várias subáreas, cada uma voltada a aspectos específicos dos espaços topológicos: topologia algébrica, topologia diferencial, topologia geral e topologia geométrica.

De modo geral, a topologia pode ser entendida tanto como o estudo das formas em sentido amplo quanto como uma disciplina matemática de caráter abstrato.

Apesar de seu caráter abstrato, os conceitos topológicos encontram aplicações concretas em diversos campos, como economia, engenharia e ciências naturais.

Espaços Topológicos

Um espaço topológico é um conjunto X munido de uma estrutura T chamada "topologia", que oferece uma base para compreender noções abstratas como continuidade, vizinhança e limite, de forma mais geral que a geometria tradicional ou a análise matemática.

$$ (X,T) $$

Exemplo: Um exemplo clássico de espaço topológico é a reta dos números reais \( \mathbb{R} \) com sua topologia usual, onde um conjunto é considerado aberto se contiver um intervalo ao redor de cada ponto. Essa construção permite estudar continuidade e limites a partir de uma perspectiva topológica.

Homeomorfismos

Um homeomorfismo é uma transformação bijetiva e contínua entre dois espaços topológicos, cujo inverso também é contínuo, garantindo a preservação das propriedades topológicas essenciais.

Na topologia, dois espaços são considerados essencialmente equivalentes se existir um homeomorfismo entre eles.

Exemplo: A transformação de uma xícara de café em uma rosquinha é o exemplo clássico de homeomorfismo. Ambos possuem um único buraco e podem ser deformados um no outro por meio de transformações contínuas, sem cortes nem colagens, preservando suas características topológicas fundamentais.

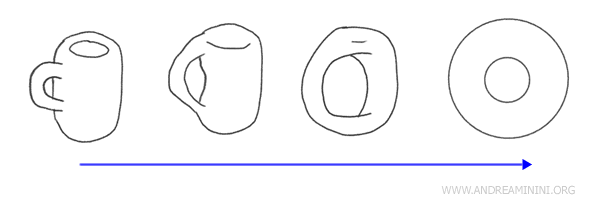
Geometria versus Topologia

Embora distintas, geometria e topologia estão interligadas, cada uma abordando aspectos diferentes dos espaços matemáticos.

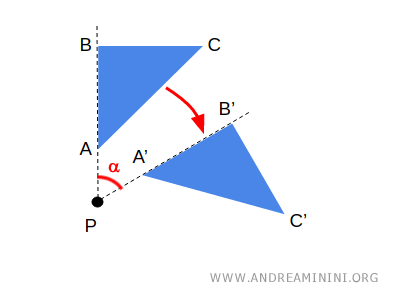
• Geometria trata das propriedades relacionadas a distâncias, ângulos e medidas, estudando figuras concretas e suas relações espaciais. Um exemplo é a rotação de uma figura, uma transformação geométrica que preserva distâncias.
  

  A geometria euclidiana é a forma mais conhecida, mas as geometrias não euclidianas investigam as consequências de flexibilizar ou negar o quinto postulado de Euclides (o postulado das paralelas).

• Topologia estuda as propriedades que permanecem mesmo quando o espaço sofre transformações contínuas, como esticar ou comprimir, sem rasgar nem colar. O interesse recai sobre aspectos qualitativos, como continuidade, conectividade e flexibilidade intrínseca das formas. Por exemplo, moldar um cubo em uma esfera mantém a conectividade entre os pontos e a continuidade global, características de uma transformação topológica.
  

  Exemplo: Um cubo de argila pode ser comprimido até se transformar em uma esfera, preservando sua continuidade e conectividade sem acréscimos ou remoções de material. Esse processo ilustra um homeomorfismo, tipo fundamental de transformação topológica.
  

Apesar das diferenças, topologia e geometria estão intimamente ligadas, sendo a topologia frequentemente vista como uma generalização da geometria.

A topologia amplia o campo de investigação para incluir propriedades mais abstratas dos espaços, em contraste com o enfoque mais restrito da geometria.

Ramos da Topologia

As aplicações da topologia se estendem a várias áreas da matemática e da ciência, e cada ramo se dedica a aspectos específicos dos espaços topológicos.

• Topologia Geométrica: Estuda propriedades preservadas por transformações como esticar, contrair e dobrar, sem rasgar nem colar. Investiga continuidade, conectividade, compacidade e fronteiras, independentemente de medidas de distância.
• Topologia Geral (ou dos Conjuntos): Analisa os espaços topológicos de forma ampla e abstrata, com foco em propriedades como conjuntos abertos e fechados, continuidade, compacidade e conectividade, além de espaços métricos e de funções.
• Topologia Algébrica: Utiliza ferramentas algébricas para estudar os espaços topológicos, relacionando estruturas algébricas às suas propriedades.
• Topologia Diferencial: Explora os espaços topológicos por meio do cálculo diferencial, em especial aqueles que localmente se assemelham ao espaço euclidiano, permitindo definir noções como tangência e diferenciabilidade.
• Topologia Aplicada: Refere-se ao uso de métodos topológicos em contextos práticos fora da matemática pura, como análise de dados, ciência de redes, engenharia e biologia computacional.

Cada ramo da topologia tem seu próprio foco, métodos e aplicações, refletindo a versatilidade e a amplitude de seus conceitos.