Fecho de um conjunto
O fecho de um conjunto \( A \) em um espaço topológico \( X \) é a interseção de todos os conjuntos fechados que contêm \( A \). Essa interseção é representada por \( \text{Cl}(A) \).
Em termos simples, o fecho de \( A \) é o menor conjunto fechado que inclui totalmente \( A \).
Não existe nenhum conjunto fechado que contenha \( A \) e seja menor do que o seu fecho.
Observação: Essa propriedade vem diretamente da definição de fecho, pois ele é construído como a interseção de todos os conjuntos fechados que contêm \( A \). Em outras palavras, o fecho reúne todos os pontos que pertencem a esses conjuntos fechados, formando o menor conjunto possível que ainda contém \( A \).
De forma formal, escrevemos:
$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ e } C \text{ é fechado em } X \} $$
Aqui, o símbolo \( \bigcap \) indica a interseção de todos os conjuntos fechados \( C \) que contêm \( A \).
O fecho de \( A \) inclui tanto os elementos do próprio conjunto quanto todos os seus pontos de acumulação dentro do espaço \( X \).
Observação: O fecho de um conjunto \( A \) depende fortemente da topologia do espaço \( X \) em que ele está inserido, e não apenas das características internas de \( A \). Por isso, o fecho pode mudar conforme a topologia considerada.
Um exemplo simples
Vamos começar com o conjunto \( A = (0, 1) \) em \( \mathbb{R} \), com a topologia usual.
Esse conjunto corresponde ao intervalo aberto entre 0 e 1, ou seja, contém todos os números reais entre esses limites, mas sem incluir as extremidades.
Nesse caso, o fecho de \( A \) é o intervalo fechado \( [0, 1] \):
$$ \text{Cl}(A) = [0,1] $$
O novo conjunto inclui todos os pontos de \( (0,1) \) e também os seus pontos de acumulação, que são 0 e 1.
Observação: Na topologia usual de \( \mathbb{R} \), um conjunto é fechado quando contém todos os seus pontos de acumulação. Um ponto é considerado de acumulação se, em qualquer vizinhança, há sempre outro ponto do conjunto. Por exemplo, a interseção dos intervalos [0,2] e [-1,1] é [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$ Nenhum intervalo fechado menor contém \( (0,1) \).
Fecho de um intervalo semiaberto
Agora, consideremos \( A = [0, 1) \) em \( \mathbb{R} \), também com a topologia usual.
Esse é um intervalo fechado à esquerda e aberto à direita, contendo todos os números de 0 (inclusivo) até 1 (exclusivo).
O fecho de \( A \) é novamente \( [0,1] \):
$$ \text{Cl}(A) = [0,1] $$
O ponto 0 já pertence a \( A \), enquanto 1 é um ponto de acumulação externo. Assim, o fecho de \( A \) precisa incluir 1 para ser fechado, resultando no conjunto \( [0,1] \).
Observação: Esse exemplo mostra claramente que o fecho de um conjunto deve incluir todos os seus pontos de acumulação. Por exemplo, a interseção de [0,2] e [-1,1] também resulta em [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$
O caso da topologia discreta
Vejamos o mesmo conjunto \( A = [0,1) \), mas agora em um espaço \( X \) com a topologia discreta.
Nessa topologia, todo subconjunto é aberto e também fechado.
- Conjunto aberto: Em um espaço discreto, qualquer subconjunto de \( X \) é aberto. Assim, \( A \) é aberto.
- Conjunto fechado: O complemento de \( A \) também é aberto, logo \( A \) é fechado.
Ou seja, todo conjunto é clopen, ao mesmo tempo aberto e fechado.
Nesse caso, o fecho de \( A \) coincide com o próprio \( A \):
$$ \text{Cl}(A) = [0,1) $$
O menor conjunto fechado que contém \( A \) é o próprio \( A \), pois ele já é fechado.
Observação: A estrutura topológica do espaço pode alterar completamente o resultado do fecho. Em um espaço discreto, como cada conjunto é fechado, o fecho nunca adiciona novos pontos.
Um exemplo em conjunto finito
Consideremos um espaço topológico \( X = \{a, b, c\} \) com a topologia discreta.
Nesse contexto, todo subconjunto de \( X \) é aberto:
- Os conjuntos \( \emptyset \) e \( \{a, b, c\} \) são abertos por definição.
- Os singletons \( \{a\} \), \( \{b\} \) e \( \{c\} \) também são abertos.
- Combinações como \( \{a, b\} \), \( \{a, c\} \) e \( \{b, c\} \) continuam sendo abertas.
Como o complemento de qualquer subconjunto também é aberto, todos os subconjuntos são simultaneamente abertos e fechados.
Se tomarmos \( A = \{b, c\} \), vemos que ele é aberto e fechado ao mesmo tempo, já que o seu complemento \( X/A = \{a\} \) também é aberto.
O fecho de \( A \), indicado por \( \text{Cl}(A) \), é a interseção de todos os conjuntos fechados que contêm \( A \). Aqui, não há nada a acrescentar:
\[ \text{Cl}(A) = \{b, c\} \]
Em uma topologia discreta, cada conjunto já é fechado, portanto o fecho é sempre igual ao conjunto original.
Observação: Para confirmar, basta observar que os conjuntos fechados que contêm \( A \) são \( \{b, c\} \) e \( \{a, b, c\} \). $$ \text{Cl}(A) = \{b, c\} \cap \{a, b, c\} = \{b, c\} $$ A interseção é exatamente \( A \), logo \( \text{Cl}(A) = A \).
O teorema do fecho de um conjunto
Em um espaço topológico \( X \), um ponto \( y \) pertence ao fecho de um subconjunto \( S \), denotado por \( \text{Cl}(S) \), se e somente se todo conjunto aberto \( U \) que contém \( y \) tem interseção com \( S \): \( y \in \text{Cl}(S) \iff \forall \ U \text{ aberto tal que } y \in U, \ U \cap S \neq \emptyset \).
Em outras palavras, um ponto \( y \) pertence ao fecho de \( S \) quando nenhuma de suas vizinhanças é completamente separada de \( S \): sempre existe, por menor que seja o aberto em torno de \( y \), ao menos um ponto de \( S \) dentro dele.
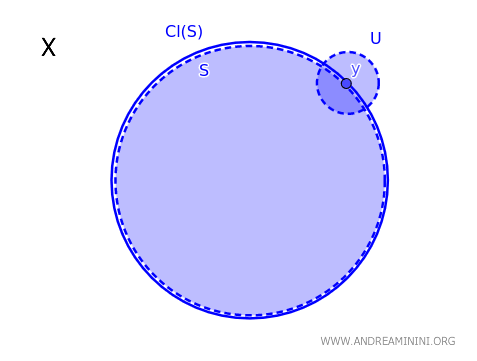
Esse resultado oferece um critério simples e poderoso para identificar quando um ponto faz parte do fecho de um conjunto em um espaço topológico.
Demonstração
- Condição necessária: Se \( y \in \text{Cl}(S) \), então, por definição, todo aberto que contém \( y \) deve intersectar \( S \). Isso ocorre porque o fecho de um conjunto inclui tanto seus pontos interiores quanto os seus pontos de acumulação. Um ponto de acumulação é aquele em cuja vizinhança sempre existe pelo menos um ponto de \( S \), que pode ser o próprio \( y \) ou outro diferente.
- Condição suficiente: Por outro lado, se todo aberto que contém \( y \) intersecta \( S \), então \( y \) é, por definição, um ponto de \( S \) ou um ponto de acumulação de \( S \). Logo, \( y \in \text{Cl}(S) \), pois não há aberto contendo \( y \) que seja totalmente disjunto de \( S \).
Observação: Este teorema é um dos pilares da topologia geral. Ele conecta diretamente a ideia de abertos à noção de fecho, sendo uma ferramenta essencial para compreender conceitos como continuidade, convergência e estrutura dos conjuntos fechados.
Exemplo prático
Considere o conjunto \( A = (0, 2) \) com a topologia usual em \( \mathbb{R} \), ou seja, o intervalo aberto dos números reais entre 0 e 2.
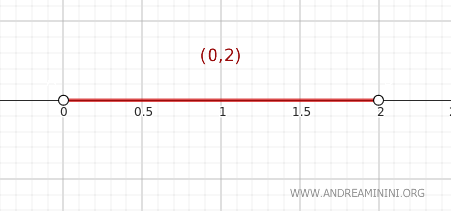
Queremos saber se o ponto \( y = 2 \) pertence ao fecho de \( A \).
Pelo teorema, \( y \in \text{Cl}(A) \) se, e somente se, todo aberto que contém \( y \) intersecta \( A \).
- Analisando as vizinhanças de \( y \): Todo intervalo aberto que contém \( y = 2 \), como \( (1{,}9, 2{,}1) \), \( (1{,}95, 2{,}05) \) ou \( (1{,}99, 2{,}01) \), inclui pontos de \( A = (0, 2) \), como \( 1{,}95 \) ou \( 1{,}99 \).
- Conclusão: Como nenhuma dessas vizinhanças é disjunta de \( A \), o ponto \( y = 2 \) pertence ao fecho de \( A \).
$$ y \in \text{Cl}(A) $$
Assim, o fecho de \( A \) é o intervalo fechado \( [0, 2] \), que inclui tanto os pontos de \( A \) quanto os seus limites, 0 e 2.
Propriedades do fecho
O operador de fecho é uma das construções mais importantes da topologia. Ele aparece em diferentes contextos e tem propriedades que ajudam a entender a estrutura dos espaços topológicos e as relações entre os conjuntos. A seguir, algumas das mais relevantes:
- Interior do complemento e complemento do fecho
O interior do complemento de um conjunto \( A \) é igual ao complemento do seu fecho: $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$ Essa propriedade expressa a relação de dualidade entre interior e fecho. - Fecho do complemento e complemento do interior
O fecho do complemento de \( A \) coincide com o complemento do seu interior: $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$ Essa relação é análoga à anterior e reforça a simetria entre os dois operadores.
Propriedades fundamentais do operador de fecho
O operador de fecho possui várias propriedades estruturais que se repetem em qualquer espaço topológico. Veja as principais:
- Preservação da inclusão em conjuntos fechados
Se \( A \subseteq C \) e \( C \) é fechado, então \( \text{Cl}(A) \subseteq C \). O fecho de um conjunto não pode ultrapassar os limites de um fechado que já o contém. - Monotonicidade
Se \( A \subseteq B \), então \( \text{Cl}(A) \subseteq \text{Cl}(B) \). O fecho preserva a relação de inclusão entre conjuntos. - Caracterização dos conjuntos fechados
Um conjunto é fechado se, e somente se, coincide com o seu próprio fecho: $$ A = \text{Cl}(A) $$ Essa propriedade fornece uma definição equivalente de conjunto fechado. - Fecho como união de pontos
O fecho de um conjunto é a união dele com o conjunto de seus pontos de acumulação: $$ \text{Cl}(A) = A \cup A' $$ Essa relação mostra como o fecho incorpora todos os limites possíveis de \( A \). - Idempotência
Aplicar o operador de fecho mais de uma vez não muda o resultado: $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$ - Inclusão
Todo conjunto está contido no seu próprio fecho: $$ A \subseteq \text{Cl}(A) $$
O conceito de fecho é essencial para compreender as ideias de continuidade, convergência e fronteira em topologia. A partir dele, é possível descrever com precisão como os conjuntos se “completam” dentro de um espaço, aproximando-se de seus limites naturais.