Conjuntos Clopen
Um conjunto clopen é aquele que, dentro de uma determinada topologia, é ao mesmo tempo aberto e fechado. Essa característica, que à primeira vista parece contraditória, é fundamental para compreender a estrutura de muitos espaços topológicos.
O nome vem da junção das palavras inglesas closed (fechado) e open (aberto). Ou seja: clopen = closed + open.
Esses conjuntos são especiais porque combinam propriedades típicas dos conjuntos abertos e dos conjuntos fechados. Em resumo, um conjunto é clopen quando tanto ele quanto o seu complemento são abertos.
Vale destacar: conjuntos clopen são raros na reta real, mas aparecem com frequência em outros espaços topológicos. Eles são importantes porque ajudam a entender a “arquitetura” de um espaço e suas propriedades mais profundas.
Exemplo passo a passo
Considere o conjunto \(X=\{a,b,c,d\}\) dentro de uma topologia \(T\).
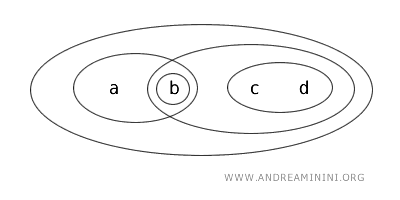
Nessa topologia, os abertos são: \(\{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, \{a,b,c,d\}, \varnothing\).
Assim, o subconjunto \(\{a,b\}\) é aberto em \(T\):
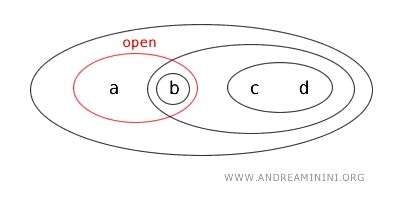
Mas note: \(\{a,b\}\) também é o complemento de \(\{c,d\}\):
$$ X - \{ c,d \} = \{a , b \} $$
Como o complemento de um aberto é fechado, concluímos que \(\{a,b\}\) também é fechado:
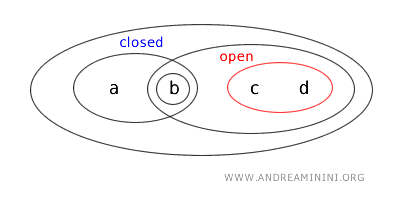
Portanto, dentro dessa topologia, \(\{a,b\}\) é aberto e fechado: um exemplo claro de conjunto clopen.
O vazio e o total: sempre clopen
Em qualquer topologia sobre um conjunto \(X\), tanto o conjunto vazio (\(\varnothing\)) quanto o conjunto total (\(X\)) são sempre clopen.
- Conjunto vazio (\(\varnothing\)): é aberto por definição. Seu complemento (\(X\)) também é aberto, logo o vazio é clopen.
- Conjunto total (\(X\)): é aberto por definição. Seu complemento (\(\varnothing\)) também é aberto, então o total também é clopen.
Isso significa que, em qualquer topologia, existem pelo menos dois conjuntos clopen garantidos: o vazio e o total.
Por que isso é relevante?
Conjuntos clopen podem parecer um detalhe técnico, mas são peças-chave para entender como funcionam as topologias. Eles revelam simetrias escondidas, ajudam a classificar espaços e aparecem em resultados importantes da matemática.
Se você gosta de explorar como conceitos aparentemente simples escondem ideias poderosas, os clopen são um ótimo ponto de partida.