Homeomorfismos em Topologia

Um homeomorfismo é uma transformação em topologia definida por uma função bijetiva e contínua, cuja inversa também é contínua.

Em outras palavras, é possível transformar um espaço em outro e depois voltar ao original sem precisar “quebrar” nem “colar” nada no processo.

De forma mais intuitiva, um homeomorfismo permite “moldar” um espaço em outro de maneira suave, sem rasgos nem junções artificiais.

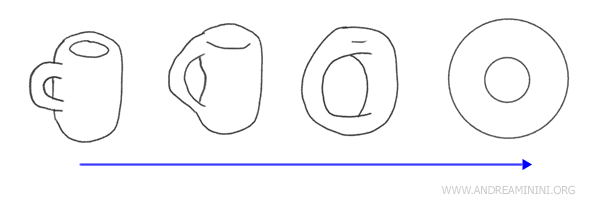
Um exemplo clássico é a comparação entre uma caneca com alça e um donut (ou toro): na topologia, eles são considerados homeomorfos. Isso porque um pode ser deformado continuamente no outro, e o inverso também é válido.

Do ponto de vista topológico, essas duas figuras são equivalentes, pois ambas possuem um único “buraco”: o furo central do donut e o espaço formado pela alça da caneca. É como se pudéssemos modelar a caneca ao redor da alça até ela se transformar em um donut.

Quando dois espaços topológicos estão relacionados por um homeomorfismo, dizemos que são "espaços homeomorfos". Isso significa que, do ponto de vista topológico, são essencialmente o mesmo espaço, mesmo que suas formas geométricas sejam diferentes.

Características de um Homeomorfismo

As principais propriedades de um homeomorfismo são:

• Função bijetiva
  Estabelece uma correspondência biunívoca entre os elementos de dois espaços: cada elemento de um corresponde a exatamente um elemento do outro, e vice-versa.
• Continuidade
  Um homeomorfismo é sempre contínuo, isto é, pequenas variações na entrada produzem pequenas variações na saída.
• Inversa contínua
  A função inversa também deve ser contínua, garantindo que a transformação possa ser revertida sem perda de continuidade.
• Preservação das propriedades topológicas
  Mantém propriedades intrínsecas como continuidade, conexidade e compacidade. Assim, as relações estruturais do espaço original são preservadas no espaço transformado.

Em resumo, um homeomorfismo é uma função contínua e invertível entre dois espaços topológicos \(X\) e \(Y\), cuja inversa também é contínua. Isso garante que as propriedades topológicas de ambos sejam preservadas.

De maneira simples, é uma forma de “remodelar” um espaço em outro sem rasgar ou colar partes. É como um "ajuste perfeito" entre duas formas ou espaços.

Vale lembrar a definição de continuidade em topologia:

Dados dois espaços topológicos \(X\) e \(Y\), uma função \(f: X \to Y\) é contínua se, para todo conjunto aberto \(V\) em \(Y\), a pré-imagem \(f^{-1}(V)\) for um conjunto aberto em \(X\).

Em outras palavras, uma função contínua em topologia “preserva” a estrutura dos conjuntos abertos ao mapear pontos de um espaço para o outro.

Portanto, a noção de continuidade em topologia é mais ampla e abstrata do que a da análise matemática.

Observação: Na análise matemática, a continuidade é definida em termos de distância entre pontos. Já na topologia, ela se baseia na estrutura dos conjuntos abertos, que é mais geral e não depende da ideia de distância.

Um Exemplo Prático

Vamos ilustrar o conceito de homeomorfismo e continuidade usando conjuntos abertos de forma bem direta.

Considere dois espaços topológicos \(X = \{a, b, c, d\}\) e \(Y = \{1, 2\}\).

• No espaço \(X\), os abertos são: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
• No espaço \(Y\), os abertos são: \(\{\}, \{1\}, \{1, 2\}\).

Uma função \(f: X \rightarrow Y\) é contínua se, para cada conjunto aberto em \(Y\), a pré-imagem for um conjunto aberto em \(X\).

Definamos \(f: X \rightarrow Y\) assim:

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).

Para visualizar, podemos representar a função \(f\) e os dois espaços topológicos destacando seus conjuntos abertos.

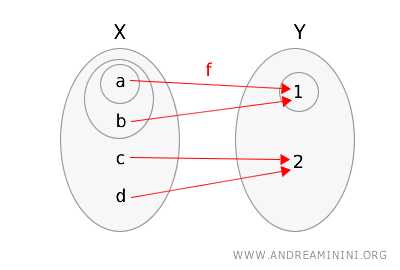
Verifiquemos se ela atende à definição de continuidade topológica.

• Para o conjunto aberto \(\{1\}\) em \(Y\), a pré-imagem é \(f^{-1}(\{1\}) = \{a, b\}\), que é aberto em \(X\).
• Para o conjunto aberto \(\{1, 2\}\) em \(Y\), a pré-imagem é \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\), também aberto em \(X\).

Como a pré-imagem de todo conjunto aberto em \(Y\) é um conjunto aberto em \(X\), a função \(f\) é contínua.

Observação: Não incluí o conjunto vazio, pois, por definição, ele é sempre aberto em qualquer espaço topológico.

Agora, considere outra função \(g: X \rightarrow Y\) definida por:

\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\).

Mais uma vez, representamos a função \(g\) e os dois espaços topológicos circulando os conjuntos abertos.

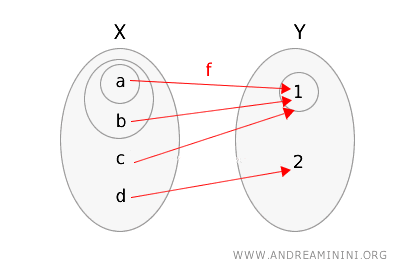
Verifiquemos se ela satisfaz a definição de continuidade topológica.

• Para o conjunto aberto \(\{1\}\) em \(Y\), a pré-imagem é \(g^{-1}(\{1\}) = \{a, b, c\}\). Esse conjunto não é aberto em \(X\).

Como existe pelo menos um conjunto aberto em \(Y\) (neste caso, \(\{1\}\)) cuja pré-imagem não é aberta em \(X\), a função \(g\) não é contínua.

Observação: Em resumo, uma função é contínua se, para todo conjunto aberto no espaço de chegada (\(Y\)), a pré-imagem em \(X\) também for aberta. Caso contrário, não é contínua. No primeiro exemplo, \(f\) é contínua porque a pré-imagem de qualquer aberto em \(Y\) é sempre um aberto em \(X\). Já \(g\) não é contínua porque isso não acontece para todos os abertos.

Definição de Homeomorfismo

Dados dois espaços topológicos \( X \) e \( Y \), e uma função bijetiva \( f: X \to Y \) com inversa \( f^{-1}: Y \to X \), se tanto \( f \) quanto \( f^{-1} \) forem contínuas, então \( f \) é um homeomorfismo, e os espaços \( X \) e \( Y \) são chamados de homeomorfos \( X \cong Y \).

Espaços homeomorfos também são conhecidos como equivalentes topológicos.

O que isso significa?

Ser homeomorfo ou equivalente topológico significa que dois espaços são “essencialmente o mesmo” do ponto de vista topológico, ainda que tenham formas geométricas diferentes.

Essa definição ressalta as condições fundamentais de um homeomorfismo:

1. Bijetividade: A função \( f: X \to Y \) deve ser injetiva e sobrejetiva, ou seja, cada elemento de \( X \) corresponde exatamente a um de \( Y \), e vice-versa.
2. Continuidade de \( f \): A função \( f \) deve ser contínua, o que significa que a pré-imagem de qualquer conjunto aberto em \( Y \) é aberta em \( X \).
3. Continuidade de \( f^{-1} \): A função inversa \( f^{-1}: Y \to X \) também precisa ser contínua, garantindo que a correspondência seja reversível sem perder as propriedades topológicas.

Exemplo: Imagine pegar uma folha de papel e enrolá-la até formar um cilindro. O cilindro e a folha plana são homeomorfos porque podemos “transformar” um no outro apenas desenrolando ou enrolando de novo - sem rasgar nem colar nada. A topologia (isto é, a estrutura dos conjuntos abertos) permanece a mesma, embora a forma geométrica seja diferente.

Vale ressaltar que a continuidade de uma bijeção \( f \) não garante automaticamente que sua inversa \( f^{-1} \) também seja contínua - a menos que \( f \) seja, além de contínua, uma aplicação aberta.

Em outras palavras: mesmo que \( f \) seja contínua e bijetiva, isso não significa, por si só, que \( f^{-1} \) seja contínua. Logo, nem toda função contínua e bijetiva é um homeomorfismo.

Na topologia, dizemos que uma função \( f: X \rightarrow Y \) é contínua se a pré-imagem de todo aberto em \( Y \) for um aberto em \( X \).

Mas essa condição não assegura que a imagem de todo aberto de \( X \), via \( f \), seja aberta em \( Y \).

Portanto, para que a inversa \( f^{-1} \) seja contínua, é necessário que \( f \) seja não apenas contínua e bijetiva, mas também uma aplicação aberta.

Exemplo

Considere os seguintes espaços topológicos:

• \( X = (a, b) \) com topologia \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
• \( Y = (1, 2) \) com topologia \( T_Y = \{\emptyset, Y\} \).

Definimos \( f: X \to Y \) por \( f(a) = 1 \) e \( f(b) = 2 \).

A função \( f \) é claramente bijetiva: cada elemento de \( X \) corresponde a um elemento único de \( Y \), e vice-versa.

Observação: No diagrama, os abertos aparecem representados por círculos. Em \( X \), além do conjunto todo, {a}, {b} e {a, b} são abertos; em \( Y \), apenas {1, 2}. O conjunto vazio, por definição aberto em qualquer topologia, não foi incluído para simplificar.

Vamos agora analisar a continuidade de \( f \) e de sua inversa \( f^{-1} \).

• Continuidade de \( f \)
  Para verificar, basta conferir se a pré-imagem de cada aberto em \( Y \) é aberta em \( X \). Como os abertos de \( Y \) são apenas \( \emptyset \) e \( Y \):
  • \( f^{-1}(\emptyset) = \emptyset \), aberto em \( T_X \)
  • \( f^{-1}(Y) = X \), aberto em \( T_X \)
  Logo, \( f \) é contínua.
• Continuidade da inversa \( f^{-1} \)
  A inversa é \( f^{-1}: Y \to X \) com \( f^{-1}(1) = a \), \( f^{-1}(2) = b \). Os abertos de \( X \) são \( \emptyset \), \(\{a\}\), \(\{b\}\) e \( X \):
  • \( f^{-1}(\emptyset) = \emptyset \), aberto em \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), não aberto em \( T_Y \)
  • \( f^{-1}(\{b\}) = \{2\} \), não aberto em \( T_Y \)
  • \( f^{-1}(X) = Y \), aberto em \( T_Y \)
  Como \(\{a\}\) e \(\{b\}\) não têm pré-imagens abertas em \( Y \), \( f^{-1} \) não é contínua.

Assim, \( f \) é bijetiva e contínua, mas sua inversa não é. Portanto, \( f \) não é um homeomorfismo.

Esse exemplo evidencia que ser contínua e bijetiva não basta: a continuidade da inversa não vem de graça.

Observação: A falha vem da diferença de granularidade das topologias: \( X \) tem abertos “finos” (\(\{a\}\), \(\{b\}\)), enquanto \( Y \) tem apenas os conjuntos mais “grosseiros” (\(\emptyset\), \(Y\)).

Exemplo 2

Agora, considere:

• \( X = (a, b) \) com topologia \( T_X = \{\emptyset, \{a\}, X\} \).
• \( Y = (1, 2) \) com topologia \( T_Y = \{\emptyset, \{1\}, Y\} \).

Definimos \( f: X \to Y \) por \( f(a) = 1 \), \( f(b) = 2 \).

Mais uma vez, \( f \) é bijetiva: cada elemento de \( X \) corresponde a um único de \( Y \).

Vamos verificar a continuidade de \( f \) e de sua inversa \( f^{-1} \).

• Continuidade de \( f \)
  Os abertos de \( Y \) são \( \emptyset \), \(\{1\}\), \( Y \):
  • \( f^{-1}(\emptyset) = \emptyset \), aberto em \( T_X \)
  • \( f^{-1}(Y) = X \), aberto em \( T_X \)
  • \( f^{-1}(\{1\}) = \{a\} \), aberto em \( T_X \)
  Logo, \( f \) é contínua.
• Continuidade da inversa \( f^{-1} \)
  Para \( f^{-1}: Y \to X \), temos \( f^{-1}(1) = a \), \( f^{-1}(2) = b \). Os abertos de \( X \) são \( \emptyset \), \(\{a\}\), \( X \):
  • \( f^{-1}(\emptyset) = \emptyset \), aberto em \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), aberto em \( T_Y \)
  • \( f^{-1}(X) = Y \), aberto em \( T_Y \)
  Portanto, \( f^{-1} \) também é contínua.

Nesse caso, \( f \) é bijetiva e contínua, e sua inversa também. Assim, \( f \) é um homeomorfismo.

A diferença em relação ao exemplo anterior está justamente na escolha das topologias de \( X \) e \( Y \).

Observação: Este exemplo mostra que, com topologias adequadas, é possível ter uma bijeção contínua cuja inversa também seja contínua - ao contrário do caso anterior, em que isso não ocorria.

Homeomorfismos e Outras Transformações Topológicas

O termo transformações topológicas é amplo, mas os homeomorfismos constituem apenas uma classe particular dentro dele.

A relação é a seguinte:

• Transformações topológicas
  São todas as transformações que alteram um espaço topológico sem destruir suas propriedades fundamentais, como continuidade e conexidade. Incluem, além dos homeomorfismos, isotopias, homotopias e difeomorfismos.
• Homeomorfismos
  São aquelas transformações que são bijetivas, contínuas e com inversa contínua. Permitem converter espaços de forma reversível, preservando integralmente a estrutura topológica. Dois espaços homeomorfos são, nesse sentido, o “mesmo” espaço topológico, apesar de eventuais diferenças geométricas.

Todo homeomorfismo é uma transformação topológica, mas nem toda transformação topológica é um homeomorfismo.

Algumas transformações preservam certas propriedades, mas não cumprem os requisitos estritos dos homeomorfismos.

Notas Finais

Alguns pontos complementares sobre homeomorfismos:

• Propriedade topológica
  É qualquer característica de um espaço que permanece inalterada sob homeomorfismos. Assim, dois espaços homeomorfos compartilham as mesmas propriedades topológicas.
• Teorema de Hausdorff
  Afirma que, se \( f: X \to Y \) é um homeomorfismo e \( X \) é de Hausdorff, então \( Y \) também será. Como os homeomorfismos preservam propriedades topológicas, \( Y \) herda a separabilidade de \( X \).
• Na álgebra abstrata, o análogo de um homeomorfismo é o isomorfismo de grupos: uma bijeção que preserva a estrutura algébrica. Já o homeomorfismo preserva a estrutura topológica dos conjuntos abertos.

E assim por diante.