A Base de uma Topologia

A base de uma topologia é um conjunto B de abertos que permite descrever toda a estrutura de um espaço topológico. Em outras palavras, qualquer conjunto aberto de T pode ser obtido como a união de alguns elementos de B.

Imagine que temos um conjunto X e uma coleção T de subconjuntos de X que definem uma topologia sobre ele. Nesse cenário, uma base da topologia T é uma coleção B de conjuntos, chamados elementos básicos, que obedecem a duas regras simples:

• Cada ponto x de X deve pertencer a pelo menos um conjunto da base B.
• Se x pertence à interseção não vazia de dois conjuntos da base, então existe um terceiro conjunto básico, contido nessa interseção, que também contém x.
  

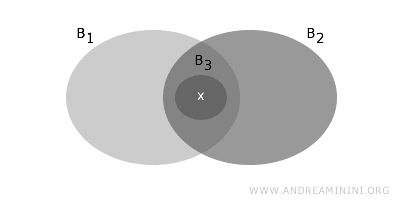
Essas condições garantem que a coleção B realmente possa gerar toda a topologia T, servindo como um ponto de partida para construir todos os abertos possíveis.

Por que isso é importante?

A ideia de base é uma ferramenta poderosa. Ela permite descrever uma topologia complexa a partir de um conjunto menor e mais simples de elementos. Em vez de listar todos os abertos, basta conhecer os conjuntos básicos, e o restante surge naturalmente como uniões desses elementos.

Nota. A condição sobre a interseção dos conjuntos básicos assegura que a topologia respeite os axiomas fundamentais: por exemplo, a interseção de dois conjuntos abertos deve continuar sendo um aberto.

Um Exemplo Concreto

Consideremos o conjunto:

$$ X = \{a, b, c \} $$

e a topologia:

$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$

Nesse caso, T contém todos os conjuntos abertos definidos sobre X. Uma base possível é:

$$ B = \{ \{ a \}, \{ b,c \} \} $$

Essa base funciona porque cada elemento de X pertence a pelo menos um conjunto de B e qualquer aberto de T pode ser obtido como a união de elementos de B:

• O conjunto {a} já está em B.
• O conjunto {b, c} também pertence a B.
• O conjunto {a, b, c} é a união dos dois:
  $$ \{ a,b,c \} = \{ a \} \cup \{ b,c \} $$

Nota. Em teoria dos conjuntos, o conjunto vazio (Ø) é sempre considerado parte da topologia, pois é um subconjunto impróprio de qualquer conjunto. Assim, $$ \emptyset \in T $$. O conjunto vazio é aberto por definição.

Este exemplo, embora simples, mostra como uma base permite representar toda a estrutura topológica de forma mais compacta. Em espaços infinitos, a construção de uma base pode ser mais sofisticada, mas a ideia essencial permanece: ela é o alicerce que sustenta todos os abertos do espaço.

Outra Forma de Construir uma Base

Podemos escolher uma base diferente para o mesmo conjunto \( X = \{a, b, c\} \):

$$ B = \{ \{ a \}, \{ b \}, \{ c \} \} $$

Aqui, a base é formada pelos conjuntos unitários, cada um contendo um único elemento de X. Vamos verificar se essa base gera a mesma topologia \( T = \{ \varnothing, X, \{a\}, \{b,c\} \} \):

• O conjunto vazio \( \varnothing \) é aberto por definição.
• O conjunto \( \{a\} \) já pertence à base.
• O conjunto \( \{b,c\} \) pode ser escrito como união de \( \{b\} \) e \( \{c\} \). $$ \{ b,c \} = \{ b \} \cup \{ c \} $$
• O conjunto total \( X = \{a,b,c\} \) é a união de todos os conjuntos da base. $$ \{ a,b,c \} = \{ a \} \cup \{ b \} \cup \{ c \} $$

Portanto, \( B \) também é uma base válida para a mesma topologia. Isso mostra que uma mesma topologia pode ter bases diferentes, dependendo de como queremos construí-la.

Nota. Diferentes bases podem gerar a mesma topologia, oferecendo maneiras distintas de representar o mesmo conjunto de abertos.

Exemplo 2: A Reta Real

Na reta real, a base da topologia usual é formada por todos os intervalos abertos:

$$ B = \{ (a,b) \subseteq \mathbb{R} \mid a < b \} $$

Essa coleção de intervalos é suficiente porque qualquer ponto da reta está contido em algum intervalo aberto \( (a,b) \).

Além disso, quando dois intervalos se sobrepõem, sua interseção também é um intervalo aberto menor, o que assegura que as condições de base sejam satisfeitas.

Por exemplo, considere os intervalos \( (0,3) \) e \( (2,4) \). Sua interseção é o intervalo \( (2,3) \), que também pertence à base:

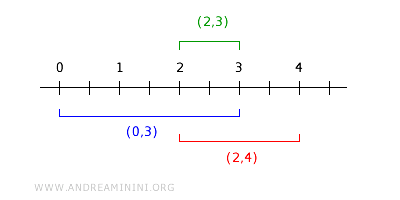
Assim, $$ (0,3) \cap (2,4) = (2,3) \in B $$. Isso confirma que a coleção de todos os intervalos abertos realmente forma uma base.

Observações Finais

Em topologia, uma base é o ponto de partida para definir e entender diferentes estruturas sobre um mesmo conjunto. Por exemplo, se criamos uma base composta por todos os conjuntos unitários \( \{x\} \), podemos gerar qualquer tipo de topologia sobre X.

Por exemplo, a base \( B = \{ \{a\}, \{b\}, \{c\} \} \) para o conjunto \( X = \{a,b,c\} \) pode gerar topologias como:

• \( T = \{ \varnothing, \{a\}, \{b,c\}, X \} \)
• A topologia trivial: \( T = \{ \varnothing, X \} \)
• A topologia discreta: \( T = \{ \varnothing, \{a\}, \{b\}, \{c\}, \{a,b\}, \{a,c\}, \{b,c\}, X \} \)

Nota. A primeira condição de base é sempre satisfeita, pois cada elemento de X está contido em pelo menos um conjunto da base. A segunda também vale, já que os conjuntos unitários são disjuntos por definição.

Esse princípio se estende a qualquer conjunto e a qualquer topologia: basta definir uma base adequada para gerar todos os abertos do espaço.