Topologie

Topologia este o ramură a matematicii care studiază proprietățile spațiilor ce rămân neschimbate sub deformări continue, precum întinderea, îndoirea sau răsucirea, atâta timp cât obiectul nu este rupt și nu este lipit.

Privită astfel, topologia se concentrează asupra acelor proprietăți geometrice care se păstrează atunci când transformările aplicate sunt continue.

Aceste proprietăți pot varia doar prin operații discontinue, de exemplu atunci când o parte a spațiului este ruptă sau când două regiuni distincte sunt conectate artificial.

Un exemplu clasic este cel al sferei și al cubului, care sunt echivalente din punct de vedere topologic. Unul poate fi transformat în celălalt printr-o deformare continuă, fără a fi necesare operații de tăiere sau de lipire.

În schimb, o sferă și un tor nu sunt echivalente topologic, deoarece trecerea de la una la cealaltă ar presupune crearea sau eliminarea unei găuri, ceea ce implică inevitabil o operație de tăiere sau de lipire.

Cu alte cuvinte, topologia se ocupă în primul rând de modul în care spațiile sunt organizate și interconectate, nu de mărimi metrice precise precum distanța, dimensiunea sau forma.

În acest cadru, noțiuni precum lungimea, aria, volumul sau măsura unghiurilor își pierd relevanța. Importante devin proprietățile calitative ale figurilor și posibilitatea de a le transforma unele în altele prin deformări continue.

Această perspectivă include, printre altele, conexitatea, compactitatea, numărul de găuri ale unui obiect, precum și alte proprietăți globale ale unui spațiu.

Topologia introduce noțiunea de spațiu topologic. Transformările sale fundamentale sunt homeomorfismele, adică aplicații continue și bijective, al căror invers este, la rândul său, continuu. Aceste transformări modifică un spațiu fără a-i altera structura topologică.

Din acest motiv, topologia este adesea descrisă drept „geometria foii de cauciuc”: obiectele sunt imaginare ca fiind realizate dintr-un material elastic, care poate fi întins, îndoit sau comprimat, dar nici rupt, nici lipit. Astăzi, topologia reprezintă un domeniu fundamental și profund unificator al matematicii contemporane.

Istorie

Dezvoltarea topologiei a început în secolul al XVIII-lea.

Originile sale sunt legate de problema Celor șapte poduri din Königsberg, abordată de Leonhard Euler, care a introdus concepte fundamentale precum conectivitatea și teoria rețelelor.

Această problemă a ridicat întrebări esențiale despre proprietățile spațiilor, punând bazele domeniului topologiei.

Problema celor șapte poduri: Pe o insulă dintr-un râu, există șapte poduri. Pornind din orice punct, este posibil să traversezi fiecare pod o singură dată? Este esențial să nu treci de două ori peste același pod.

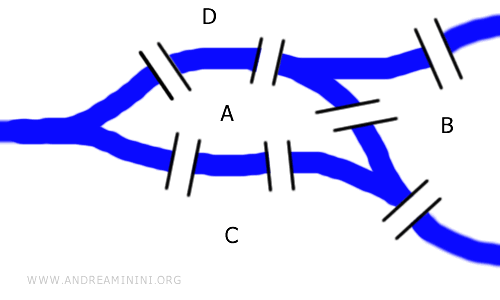
Această provocare nu implică măsurarea distanțelor sau a lungimilor podurilor; este, în esență, o problemă topologică ce poate fi reprezentată prin intermediul grafurilor. Graful prezentat aici este echivalent topologic cu dispunerea originală a podurilor.

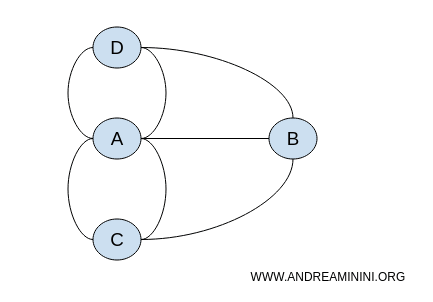
Pozițiile nodurilor din graf nu au relevanță. Importantă este conexiunea dintre noduri. Prin urmare, problema poate fi reprezentată printr-un număr infinit de grafuri diferite, dar echivalente topologic.

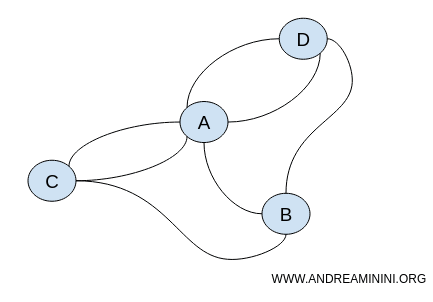
Ambele grafuri păstrează aceleași proprietăți topologice, cum ar fi continuitatea și conectivitatea.

Euler a demonstrat că problema celor șapte poduri din Königsberg, deși geometrică, nu depinde de măsurarea dimensiunilor.

El a arătat că provocarea ținea de poziție și a demonstrat că este imposibil de rezolvat, punând astfel bazele conceptului de „geometrie a poziției”.

De-a lungul secolului al XIX-lea, matematicieni precum Carl Friedrich Gauss, August Ferdinand Möbius, Johann Listing, Bernhard Riemann și Felix Klein au studiat proprietățile formelor și suprafețelor, aprofundând înțelegerea proprietăților topologice.

Notă: Johann Listing a fost cel care a introdus pentru prima dată termenul „topologie” în 1847, însă acesta a devenit larg acceptat în comunitatea științifică abia după câteva decenii.

În secolul al XIX-lea, geometria poziției a fost aplicată în domenii practice, precum analiza rețelelor electrice, datorită contribuțiilor lui Gustav Kirchhoff.

Ulterior, Henri Poincaré, la sfârșitul secolului al XIX-lea și începutul secolului XX, a adus contribuții semnificative în domeniul topologiei algebrice prin studiile sale.

În secolul XX, topologia s-a ramificat în domenii specializate precum topologia algebrică și topologia generală, cu contribuții notabile de la matematicieni precum Felix Hausdorff, Cantor și Brouwer, mai ales în domeniul matematicii abstracte.

Astăzi, topologia reprezintă un domeniu fundamental al matematicii, axat pe studiul proprietăților ce rămân neschimbate sub transformări continue.

Topologia include acum numeroase subdiscipline, fiecare concentrându-se pe aspecte specifice ale spațiilor topologice, precum topologia algebrică, topologia diferențială, topologia generală și topologia geometrică.

În ansamblu, topologia poate fi privită ca o explorare generală a formelor și, în mod teoretic, ca o disciplină abstractă a matematicii.

În ciuda caracterului său abstract, conceptele topologice își găsesc aplicații în diverse domenii practice, precum economia, ingineria și știința.

Spații Topologice

Un spațiu topologic este un set X, echipat cu o structură T numită „topologie”, care oferă un cadru pentru înțelegerea conceptelor abstracte precum continuitatea, apropierea și limitele, într-o manieră mai generală decât geometria sau analiza matematică tradițională.

$$ (X,T) $$

Exemplu: Un exemplu clasic de spațiu topologic este linia numerelor reale \( \mathbb{R} \), cu topologia sa standard, unde un set este deschis dacă include un interval în jurul fiecărui punct. Această configurație facilitează studierea continuității și a limitelor dintr-o perspectivă topologică.

Homeomorfisme

Un homeomorfism este o transformare bijectivă și continuă între două spații topologice, a cărei inversă este și ea continuă, păstrând astfel proprietățile topologice fundamentale.

Două spații sunt considerate echivalente din punct de vedere topologic dacă există un homeomorfism între ele.

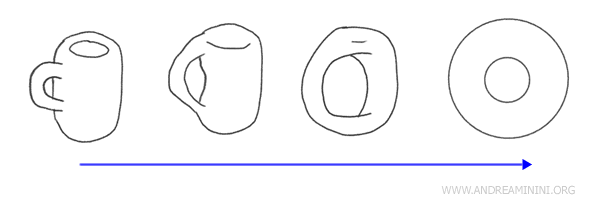
Exemplu: Transformarea unei cești de cafea într-un covrig este un exemplu clasic de homeomorfism. Ambele obiecte au o singură gaură și pot fi deformate continuu unul în celălalt fără a tăia sau lipi materialul, păstrându-și caracteristicile topologice fundamentale.

Geometrie versus Topologie

Deși geometria și topologia sunt domenii distincte, ele sunt strâns legate, fiecare concentrându-se pe aspecte diferite ale spațiilor matematice.

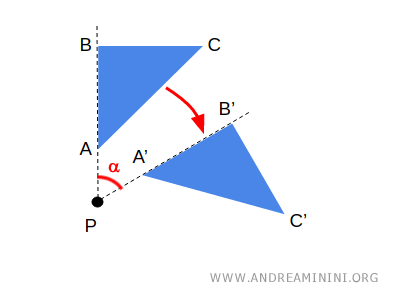
• Geometria studiază proprietăți legate de distanțe, unghiuri și măsurători, concentrându-se pe figuri concrete și relațiile lor spațiale. Un exemplu este rotația unei figuri, o transformare geometrică ce păstrează distanțele.
  

  Geometria euclidiană este cea mai cunoscută formă, însă geometria non-euclidiană explorează implicațiile relaxării sau eliminării celui de-al cincilea postulat al lui Euclid (postulatul paralelelor).

• Topologia se concentrează pe proprietăți care rămân invariabile sub transformări continue, cum ar fi întinderea sau comprimarea, fără tăiere sau lipire. Ea analizează aspecte calitative, cum ar fi continuitatea, conectivitatea și flexibilitatea inerentă a formelor. De exemplu, transformarea unui cub într-o sferă păstrează conectivitatea punctelor și continuitatea generală, caracteristici tipice ale unei transformări topologice.
  

  Exemplu: Un cub din lut poate fi modelat într-o sferă prin comprimare, păstrându-și continuitatea și conectivitatea fără a adăuga sau elimina material. Acest exemplu ilustrează un homeomorfism, o transformare fundamentală în topologie.
  

În ciuda diferențelor, topologia și geometria sunt domenii strâns corelate, topologia fiind adesea considerată o generalizare a geometriei.

Topologia extinde aria de studiu pentru a include proprietăți abstracte ale spațiilor, în contrast cu abordarea mai concretă a geometriei.

Ramurile Topologiei

Topologia are aplicații variate în matematică și știință, fiecare ramură concentrându-se pe aspecte unice ale spațiilor topologice.

• Topologia geometrică: Această ramură studiază proprietățile păstrate în urma transformărilor precum întinderea, comprimarea și plierea, fără tăiere sau lipire. Analizează continuitatea, conectivitatea, compactitatea și limitele, ignorând distanțele.
• Topologia generală (sau a mulțimilor punctuale): Studiază spațiile topologice într-un mod abstract, concentrându-se pe proprietăți precum mulțimile deschise și închise, continuitatea, compactitatea și conectivitatea, precum și pe spațiile metrice și funcționale.
• Topologia algebrică: Utilizează instrumente algebrice pentru a studia spațiile topologice, legând structurile algebrice de acestea pentru o înțelegere mai profundă.
• Topologia diferențială: Aplică calculul diferențial pentru a analiza proprietățile și structurile spațiilor care seamănă local cu spațiul euclidian, introducând concepte precum tangenta și diferențiabilitatea.
• Topologia aplicată: Această ramură se ocupă de utilizarea conceptelor topologice în aplicații practice, cum ar fi analiza datelor, știința rețelelor, ingineria și biologia computațională.

Fiecare ramură a topologiei are propriile metode și aplicații, reflectând versatilitatea acestui domeniu.