Topologia uzuală a unei mulțimi deschise

Topologia uzuală (sau naturală) pe $ \mathbb{R} $ este construită pornind de la intervalele deschise $ (a, b) $, cu $ a < b $, precum și de la orice reuniune, finită sau infinită, a unor astfel de intervale. Aceste intervale formează baza mulțimilor deschise din topologia standard.

Mai exact, o mulțime $ U $ este considerată deschisă dacă, pentru fiecare punct $ x \in U $, există un interval deschis $ (a, b) $ astfel încât $ x \in (a, b) $ și $ (a, b) \subseteq U $.

$$ x \in (a,b) \subseteq U $$

Asta înseamnă că fiecare punct al unei mulțimi deschise se află într-un interval deschis complet inclus în acea mulțime.

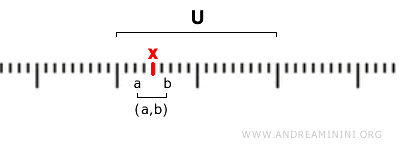
reprezentare a unei mulțimi deschise în topologia uzuală

În topologia uzuală, următoarele tipuri de mulțimi sunt considerate deschise:

Intervale deschise
Toate intervalele deschise $ (a, b) $, cu $ a < b $, sunt mulțimi deschise, precum și orice reuniune, finită sau infinită, a unor astfel de intervale.
Operații cu mulțimi deschise
În această topologie, reuniunile și intersecțiile finite de mulțimi deschise păstrează proprietatea de deschidere.
- Reuniuni: Orice reuniune, chiar infinită, de mulțimi deschise rămâne deschisă.
- Intersecții finite: Intersecția unui număr finit de mulțimi deschise este tot o mulțime deschisă.

Topologia uzuală este una dintre cele mai importante topologii pe un ansamblu $ X $. Este denumită „uzuală” sau „naturală” pentru că este cea mai folosită și are un rol central în analiza matematică și în teoria continuității.

Este preferată pentru că surprinde într-un mod intuitiv conceptele de apropiere, deschidere și continuitate, în special pe linia reală $ \mathbb{R} $.

Observație: Pe $ \mathbb{R} $ și pe alte spații există și topologii alternative, construite pe baze diferite. Acestea definesc mulțimi deschise după alte reguli și sunt utilizate pentru a studia proprietăți particulare sau pentru a explora structuri matematice dintr-o perspectivă diferită.

Exemplu practic

Baza topologiei uzuale pe $ \mathbb{R} $ este formată din toate intervalele deschise $ (a, b) $, cu $ a < b $.

$$ B = \{ (a,b) \subset \mathbb{R} \ | \ a<b \} $$

O caracteristică esențială a acestei topologii este următoarea: pentru orice punct $ x $ care aparține unei mulțimi deschise $ U $, există întotdeauna un interval deschis centrat în $ x $, complet conținut în $ U $. Această proprietate respectă definiția formală a unei mulțimi deschise în topologia uzuală.

$$ \forall \ x \in U \ \exists \ \epsilon>0 \ | \ (x-\epsilon, x+\epsilon) \subseteq U $$

Prin urmare, $ U $ este o mulțime deschisă în topologia uzuală pe $ \mathbb{R} $.

Se folosește termenul „topologie uzuală” pentru că aceasta este topologia de referință pe axa reală, utilizată pentru definirea riguroasă a noțiunilor de limită și continuitate.

Exemplul 2

Considerăm intervalul $ (0,1) $, care nu include capetele $ 0 $ și $ 1 $, și analizăm structura sa topologică în raport cu topologia uzuală.

Întrebarea este dacă acest interval poate fi privit ca un spațiu topologic propriu.

reprezentare topologică a intervalului (0,1)

În topologia indusă, o submulțime $ U \subset (0,1) $ este deschisă în $ (0,1) $ dacă, pentru fiecare punct $ x \in U $, există un interval deschis $ (a, b) $ din $ \mathbb{R} $ astfel încât $ x \in (a, b) $ și $ (a, b) \cap (0,1) \subseteq U $.

Observăm că intervalul $ (0,1) $ poate fi exprimat ca intersecția mai multor mulțimi deschise din topologia uzuală a lui $ \mathbb{R} $, ceea ce înseamnă că el moștenește o structură topologică clar definită.

Așadar, intervalul $ (0,1) $ este un spațiu topologic dotat cu topologia indusă de topologia naturală a lui $ \mathbb{R} $.

De exemplu, intervalele $ (0.1, 0.5) $, $ (0.2, 0.9) $ sau reuniunea lor, precum $ (0.1, 0.5) \cup (0.6, 0.8) $, sunt mulțimi deschise în $ (0,1) $ pentru topologia indusă. Cu alte cuvinte, mulțimile deschise din $ (0,1) $ sunt exact acele mulțimi deschise din $ \mathbb{R} $ a căror intersecție cu $ (0,1) $ este complet inclusă în acest interval.

Deoarece $ (0,1) $ este un subspațiu topologic al lui $ \mathbb{R} $, el moștenește toate proprietățile fundamentale ale acestuia.

Exemplul 3

Să analizăm mulțimea finită $ X = \{1,2,3\} $, alcătuită din trei numere naturale.

Întrebarea este dacă putem dota $ X $ cu o structură topologică derivată din topologia standard a lui $ \mathbb{R} $.

În acest caz, elementele izolate ale lui $ X $ nu pot fi considerate deschise, deoarece baza topologiei standard este alcătuită din intervale deschise, ceea ce nu se aplică unei mulțimi discrete precum $ X $.

De exemplu, dacă luăm elementul $ \{2\} $ din $ X $, îl putem include într-un interval deschis $ (2-\epsilon, 2+\epsilon) $, dar acel interval conține o infinitate de numere reale care nu fac parte din $ X $. Prin urmare, $ \{2\} $ nu poate fi o mulțime deschisă în topologia standard a lui $ \mathbb{R} $.
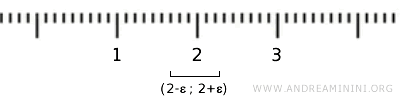
exemplu cu elementul 2 în topologia standard

Dacă privim $ X $ ca pe un subansamblu al lui $ \mathbb{R} $, „topologia indusă” sau „topologia subspațiului” pe $ X $ conține doar două mulțimi deschise: mulțimea vidă și mulțimea $ X $ însăși, ceea ce reprezintă o structură topologică trivială.

Pentru a conferi unei mulțimi finite precum $ X $ o structură topologică mai bogată, se folosește de obicei topologia discretă, în care toate submulțimile lui $ X $ sunt deschise prin definiție.

Astfel de exemple ajută la înțelegerea modului în care alegerea topologiei influențează proprietățile unui spațiu matematic.