Mulțimi deschise în topologie

O mulțime A se numește deschisă dacă, pentru fiecare element x din A (x∈A), există o vecinătate a lui x care se află în întregime în interiorul mulțimii.

 

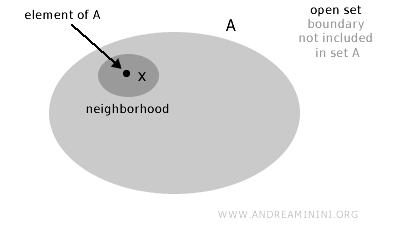
Intuitiv, o mulțime este deschisă atunci când nu conține punctele aflate chiar pe marginea ei. Punctele din interior au întotdeauna un „spațiu de manevră", fără să atingă frontiera.

Formal, o mulțime A dintr-un spațiu topologic X este deschisă dacă, pentru fiecare punct x din A, putem găsi o vecinătate aflată complet în interiorul lui A.

Notă. Această idee garantează că în jurul fiecărui punct al mulțimii există o regiune care nu iese în afara ei.

Un exemplu ușor de vizualizat

Pe axa reală, cel mai simplu exemplu de mulțime deschisă este un interval deschis.

Ce este un interval deschis? Un interval deschis în R este mulțimea tuturor numerelor reale x care satisfac a

Notăm acest interval (a,b). Parantezele arată că valorile a și b nu sunt incluse în mulțime.

De exemplu, intervalul deschis (3,10) este o mulțime deschisă în R.

El conține o infinitate de numere reale aflate strict între 3 și 10.

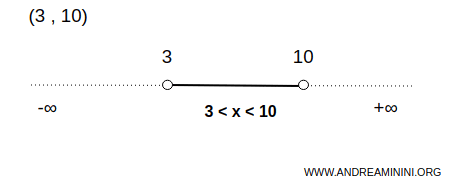
Orice punct din interior are propriul său interval deschis complet inclus în (3,10).

De exemplu, pentru x=3.1 putem lua intervalul (3.09,3.11), care rămâne în întregime în interiorul intervalului dat.

Pentru orice x din interval, situația este aceeași, deoarece între două numere reale există întotdeauna o infinitate de alte numere reale.

Notă. Chiar și pentru un număr foarte apropiat de 3 sau 10, putem găsi mereu o vecinătate suficient de mică aflată în interiorul mulțimii. Conceptul rămâne valabil indiferent cât de „strâns" privim intervalul.

Acesta este un exemplu unidimensional tipic de mulțime deschisă.

Exemple în dimensiuni mai mari

Ideea se extinde natural și în plan.

Considerăm mulțimea punctelor aflate în interiorul unui disc cu raza r=1 și centrul în origine (0,0).

$$ x^2+y^2<1 $$

Această condiție include toate punctele din interiorul cercului și le exclude pe cele aflate pe circumferință.

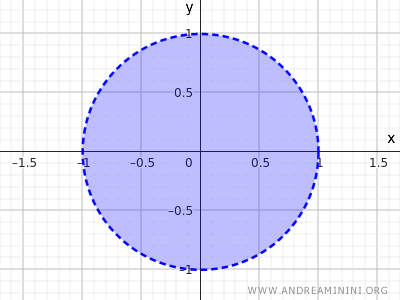
Și acesta este un exemplu de mulțime deschisă.

Când vorbim despre o mulțime închisă?

Dacă includem și punctele aflate pe frontieră, obținem o mulțime închisă:

$$ x^2+y^2 \le 1 $$

Aici, punctele de pe margine nu mai au vecinătăți aflate complet în interiorul mulțimii.

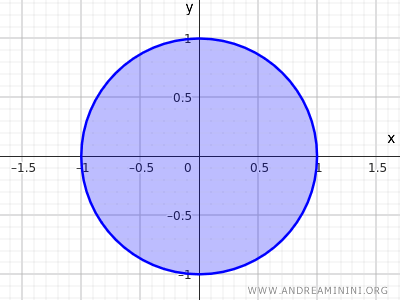
Așadar, condiția pentru mulțimile deschise nu mai este îndeplinită.

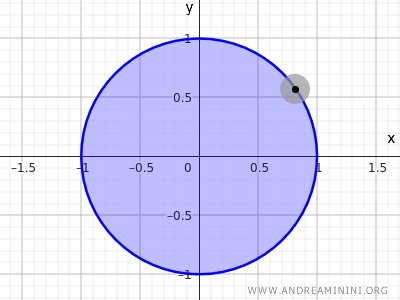
Notă. Mulțimea definită doar de ecuația \(x^2+y^2=1\) nu este nici deschisă, nici închisă în R², deoarece conține doar punctele de pe frontieră, fără interior. Prin comparație, \(x^2+y^2<1\) este deschisă, iar \(x^2+y^2\le 1\) este o mulțime închisă.

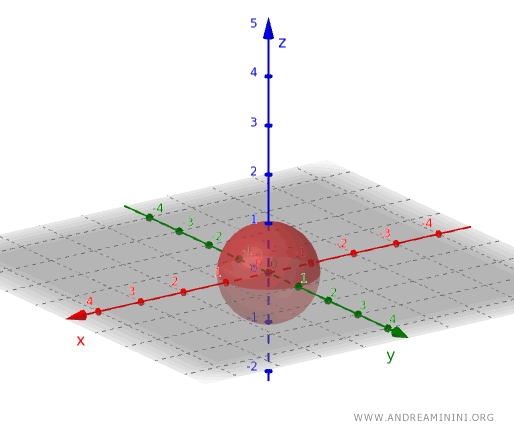
Prin același principiu, în spațiul tridimensional obținem o mulțime deschisă dacă luăm toate punctele din interiorul unei sfere, fără punctele de pe suprafață.

Dependența de topologie

Intervalele deschise sunt utile pentru a construi intuiția, dar în topologie noțiunea de mulțime deschisă este mult mai generală.

Pentru a înțelege pe deplin conceptul, trebuie ținut cont de topologia aleasă pentru spațiul respectiv.

Noțiunea de „mulțime deschisă" depinde de topologie.

Cu alte cuvinte, ce este sau nu deschis depinde de regulile topologiei definite pe acel spațiu.

Ce este o topologie? O topologie este o colecție de mulțimi declarate „deschise" care respectă anumite reguli, cum ar fi: reuniunea oricăror mulțimi deschise este deschisă, iar intersecția unui număr finit de mulțimi deschise este și ea deschisă.

Așadar, nu trebuie să ne limităm la intervale sau discuri atunci când vorbim despre mulțimi deschise.

În topologie, există multe alte exemple, uneori surprinzătoare.

Un exemplu simplu

Considerăm spațiul \( \{a, b\} \), format din doar două elemente.

Pe acest spațiu putem defini cel puțin două topologii: topologia trivială și topologia discretă.

• Topologia trivială
  Singurele mulțimi deschise sunt mulțimea vidă \( \emptyset \) și spațiul întreg \( \{a, b\} \).
• Topologia discretă
  Toate submulțimile lui \( \{a, b\} \) sunt deschise. Astfel, \( \{a\} \), \( \{b\} \), \( \{a, b\} \) și \( \emptyset \) sunt toate considerate deschise.

Analizăm acum submulțimea \( \{a\} \):

• În topologia trivială, mulțimea {a} nu este deschisă, deoarece singurele mulțimi deschise sunt \( \{a,b\} \) și \( \emptyset \).
• În topologia discretă, mulțimea {a} este deschisă, deoarece orice submulțime este deschisă prin definiție.

Acest exemplu arată clar cât de mult depinde noțiunea de mulțime deschisă de topologia aleasă.

Teorema mulțimilor deschise

Teorema 1

Considerăm un spațiu topologic (X,T), unde T este o topologie pe mulțimea X. Un subansamblu S ⊂ X este deschis dacă pentru fiecare punct s ∈ S există o vecinătate U inclusă complet în S, adică U ⊂ S.

Această proprietate este de fapt criteriul fundamental care definește mulțimile deschise într-o topologie.

Putem privi fiecare punct s ∈ S ca fiind înconjurat de o zonă de siguranță U_s, aflată în întregime în interiorul lui S. Această idee conduce la relația:

$$ x \in U_s \subset S \subset X $$

Rezultă că o mulțime deschisă poate fi interpretată ca reuniunea tuturor vecinătăților deschise ale punctelor sale.

În concluzie, o mulțime este deschisă dacă și numai dacă fiecare punct din interiorul ei are o vecinătate complet inclusă în mulțime.

Exemplu intuitiv. Imaginăm o masă acoperită cu bile de sticlă. Fiecare bilă reprezintă un punct dintr-o mulțime. Dacă pot desena în jurul fiecărei bile un cerc care rămâne în întregime pe suprafața mesei, fără a atinge marginile, atunci mulțimea acestor bile poate fi considerată deschisă. Fiecare punct are spațiul său propriu în interiorul mulțimii, fără contact cu exteriorul.

Teorema 2

Fie \( X \) o mulțime și \( B \) o bază pentru o topologie pe \( X \). Un subansamblu \( A \subset X \) este deschis în topologia generată de \( B \) dacă și numai dacă pentru fiecare element \( x \in A \) există un set de bază \( B_x \in B \) care îl conține și este complet inclus în \( A \), adică \( B_x \subseteq A \).

Teorema evidențiază ideea centrală a topologiilor construite pe baza unei colecții de mulțimi fundamentale. Fiecare punct al lui \( A \) trebuie să fie acoperit de o vecinătate din bază, aflată integral în interiorul lui \( A \).

Demonstrație. Dacă \( A \) este deschisă în topologia generată de baza \( B \), atunci prin definiție ea este reuniunea elementelor de bază din \( B \). Fiecare punct \( x \in A \) aparține cel puțin unei astfel de mulțimi \( B_x \), care este inclusă în \( A \). Raționamentul funcționează și în sens invers. Dacă pentru fiecare punct \( x \in A \) există un element de bază \( B_x \subseteq A \), rezultă că \( A \) este deschisă în topologia generată de \( B \).

Exemplu practic

Considerăm mulțimea \( X = \{1, 2, 3, 4, 5\} \) și baza \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \). Vrem să verificăm dacă \( A = \{1, 2, 3\} \) este deschisă.

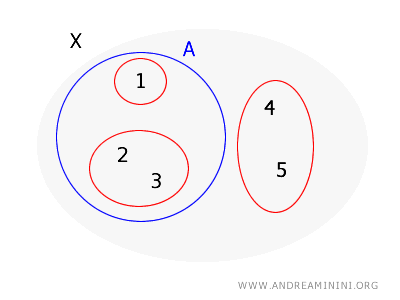
Analizăm fiecare punct din \( A \):

• Pentru 1, elementul \( \{1\} \) este inclus în întregime în \( A \).
• Pentru 2, elementul \( \{2, 3\} \) este inclus în întregime în \( A \).
• Pentru 3, aceeași mulțime \( \{2, 3\} \) funcționează perfect.

Fiecare punct din \( A \) este acoperit de un element al bazei inclus în \( A \). Concluzia este clară: \( A \) este deschisă.

Exemplu 2

Luăm aceeași bază și analizăm acum mulțimea \( A = \{2, 3, 4\} \).

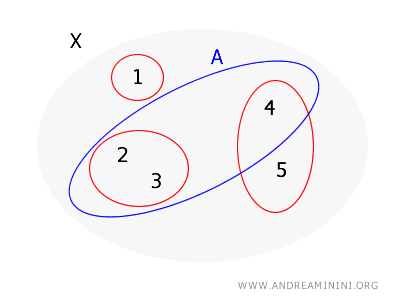
În acest caz:

• Pentru 2, \( \{2, 3\} \) este inclusă în \( A \).
• Pentru 3, situația este aceeași.
• Pentru 4 însă, singura mulțime din bază care îl conține este \( \{4, 5\} \), care nu este inclusă în întregime în \( A \), deoarece conține elementul 5.

Rezultatul este următorul: \( A \) nu este deschisă în topologia generată de \( B \).

Note suplimentare

Iată o proprietate importantă legată de mulțimile deschise:

• O mulțime A este deschisă dacă și numai dacă A = Int(A)
  Interiorul unei mulțimi \( A \), notat Int(A), este definit ca reuniunea tuturor mulțimilor deschise conținute în \( A \). Această proprietate se exprimă prin relația $$ A = \text{Int}(A) $$

Aceste concepte stau la baza topologiei și vor reapărea frecvent în studiul structurilor spațiale.