Mulțimi închise

Spunem că o mulțime $ B $ dintr-un spațiu topologic $ X $ este închisă dacă pentru orice element din complementara $ u \in X - B $ există un vecinaj aflat în întregime în complementara $ X - B $.
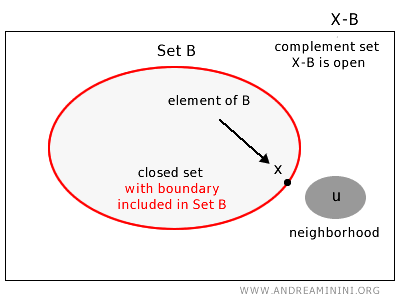
exemplu de mulțime închisă

Cu alte cuvinte, o mulțime este închisă atunci când conține toate punctele sale de frontieră.

În mod riguros, o mulțime $ B $ dintr-un spațiu topologic $ X $ este închisă dacă și numai dacă mulțimea complementară $ X - B $ este deschisă.

Observație: Acest lucru implică faptul că în $ B $ există puncte pentru care niciun vecinaj nu poate fi inclus în întregime în interiorul mulțimii.

Un exemplu concret
Complementara unei mulțimi închise
Exemplu
Proprietăți ale mulțimilor închise
Exemple
Observații suplimentare

Un exemplu concret

Să considerăm dreapta reală $ \mathbb{R} $ și un interval închis.

Ce este un interval închis? Un interval închis din $ \mathbb{R} $ este format din toate punctele $ x $ care satisfac $ a \leq x \leq b $, unde $ a $ și $ b $ sunt numere reale cu $ a < b $, iar capetele sunt incluse în interval.

Un astfel de interval se notează $[a,b]$, iar parantezele pătrate indică apartenența extremităților $ a $ și $ b $ la mulțime.

De exemplu, intervalul $[3,10]$ reprezintă o mulțime închisă pe dreapta reală $ \mathbb{R} $.

Așadar, mulțimea $ B $ cuprinde toate valorile numerice între 3 și 10, incluzând capetele intervalului.

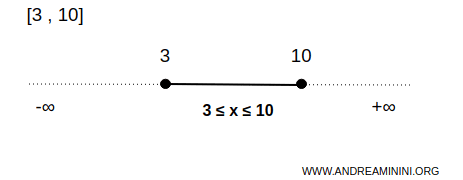
exemplu de interval închis

Prin urmare, orice punct $ x $ cu $ 3 \leq x \leq 10 $ aparține mulțimii, inclusiv $ x = 3 $ și $ x = 10 $.

Totuși, nu toate punctele din acest interval admit un vecinaj care să fie conținut în întregime în $[3,10]$.

De exemplu, orice vecinaj al punctului $ x = 3 $ va conține inevitabil și valori mai mici decât 3, care nu aparțin intervalului.

Observație: Chiar și un vecinaj extrem de mic, precum $ 3 \pm 0{,}00000001 $, nu poate fi inclus integral în $[3,10]$, deoarece $ 3 - 0{,}00000001 < 3 $. Situația este identică pentru $ x = 10 $, unde niciun vecinaj nu poate rămâne complet în interiorul intervalului.

Acesta este un exemplu elementar de mulțime închisă într-un spațiu unidimensional.

Alte exemple de mulțimi închise

Extindem acum ideea în plan ($\mathbb{R}^2$).

Considerăm mulțimea punctelor din interiorul unui disc de rază $ r = 1 $, cu centrul în $(0,0)$:

$$ x^2 + y^2 \leq 1 $$

Această inegalitate descrie toate punctele situate la o distanță cel mult 1 față de centru, incluzând atât interiorul discului, cât și punctele de pe cerc.

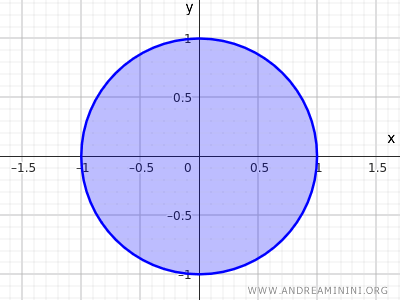
exemplu de mulțime închisă în plan

Avem, așadar, un nou exemplu de mulțime închisă.

Observăm că punctele de pe circumferința definită de $ x^2 + y^2 = 1 $ nu admit vecinaje care să fie conținute în întregime în discul închis.

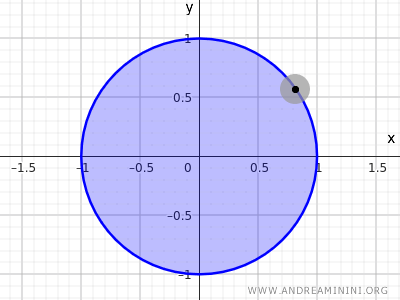
exemplu suplimentar de mulțime închisă

Observație: În topologie, mulțimea definită de $ x^2 + y^2 = 1 $ nu este nici deschisă, nici închisă în $ \mathbb{R}^2 $, deoarece conține doar punctele de pe cerc și exclude interiorul. În schimb, mulțimea $ x^2 + y^2 \leq 1 $, care include interiorul împreună cu punctele de pe frontieră, este un exemplu tipic de mulțime închisă deoarece reține toate punctele sale de margine.

Aceeași idee se aplică și în spațiul tridimensional, pentru o sferă plină, precum și în spațiul $ n $-dimensional, pentru o $ n $-sferă închisă.

Complementara unei mulțimi închise

Într-un spațiu topologic $ X $, complementara unei mulțimi închise $ C $ este o mulțime deschisă, notată $ X - C $.

Prin urmare, dacă $ C $ este închisă în $ X $, atunci $ X - C $ este, în mod necesar, deschisă.

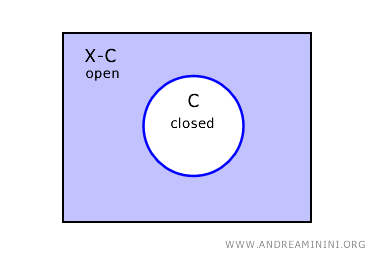
complementul unei mulțimi închise

Reciproc, dacă o mulțime $ U $ este deschisă, atunci complementara $ X - U $ este închisă.

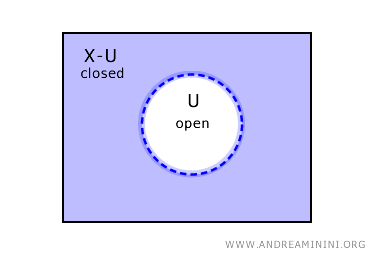
complementul unei mulțimi deschise

Totuși, acestea nu sunt singurele situații. În anumite spații topologice pot exista mulțimi care sunt simultan deschise și închise, precum și mulțimi care nu sunt nici deschise, nici închise.

Așadar, faptul că o mulțime nu este închisă nu implică automat că este deschisă, iar o mulțime care nu este deschisă nu este neapărat închisă.

Exemplu

Considerăm un spațiu topologic $ (X, T) $ în care mulțimea $ X = \{a,b,c,d\} $ conține patru elemente, iar topologia $ T $ este formată din următoarele mulțimi deschise:

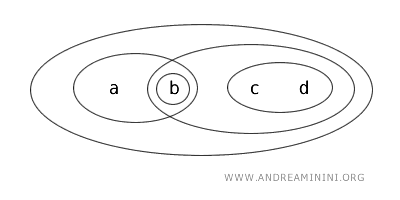
exemplu practic

Mulțimile deschise ale acestei topologii sunt: $ \{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, X $ și mulțimea vidă $ \varnothing $.

Să analizăm câteva cazuri:

Mulțimea $ \{b\} $ este deschisă, deoarece apare explicit în topologie.
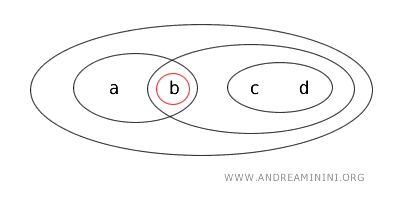
Mulțimea $ \{a\} $ este închisă, deoarece complementara sa este o mulțime deschisă. Într-adevăr, $ X - \{a\} = \{b,c,d\} $ este deschisă.
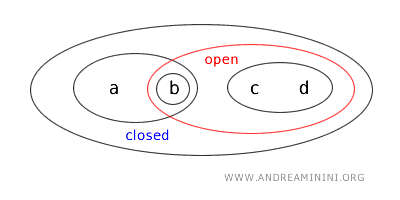
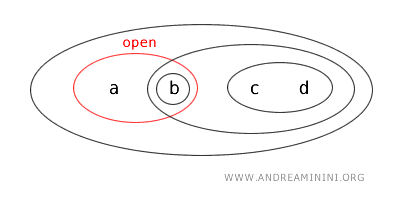
Mulțimea $ \{a,b\} $ este atât deschisă, cât și închisă (clopen). Deși astfel de situații sunt rare în topologiile clasice pe $ \mathbb{R} $, ele apar în spații mai generale. Aici, $ \{a,b\} $ este deschisă prin definiție, iar complementara $ X - \{a,b\} = \{c,d\} $ este tot deschisă, ceea ce o face simultan închisă.
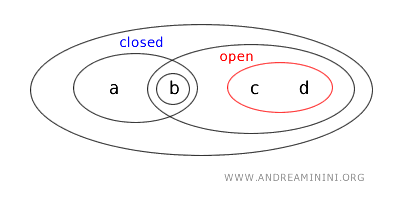
Mulțimea $ \{b,c\} $ nu este nici deschisă, nici închisă. Nu figurează în lista mulțimilor deschise, iar complementara $ X - \{b,c\} = \{a,d\} $ nu este deschisă. Prin urmare, mulțimea nu îndeplinește criteriile pentru niciuna dintre categorii.

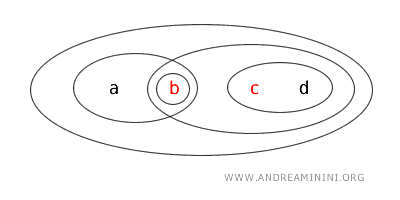
Acest exemplu evidențiază clar faptul că într-un spațiu topologic o mulțime poate fi deschisă, închisă, ambele simultan sau niciuna dintre acestea.

Proprietăți ale mulțimilor închise

O mulțime închisă este, în esență, complementara unei mulțimi deschise. Printre proprietățile fundamentale ale mulțimilor închise se numără:

Mulțimea vidă ($\varnothing$) și întregul spațiu $ X $ sunt întotdeauna închise.
Intersecția oricărei colecții (finite sau infinite) de mulțimi închise este la rândul ei o mulțime închisă.
Reuniunea unui număr finit de mulțimi închise rămâne o mulțime închisă.

Exemple

În topologia uzuală a spațiului euclidian $ \mathbb{R}^n $, orice punct izolat formează o mulțime închisă.

Dacă alegem un punct $ n $ pe dreapta reală ($ \mathbb{R}^1 $), complementara acestuia este mulțimea tuturor punctelor din $ \mathbb{R}^1 $, cu excepția lui $ n $.

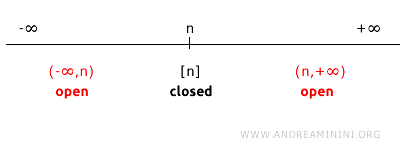
exemplu de mulțime închisă în spațiul real

Complementara mulțimii $\{n\}$ este reuniunea a două intervale deschise: $(-\infty, n) \cup (n, +\infty)$.

Deoarece intervalele $(-\infty, n)$ și $(n, +\infty)$ sunt deschise în topologia standard, reuniunea lor $(-\infty, n) \cup (n, +\infty)$ este tot o mulțime deschisă.

Prin urmare, $\{n\}$ este o mulțime închisă, deoarece complementara sa este deschisă.

Totuși, în alte topologii, punctele izolate nu sunt neapărat mulțimi închise. Totul depinde de structura topologică a spațiului considerat.

Să analizăm o topologie pe $ \mathbb{R} $, generată de intervalele deschise $ (n, n+1) $ pentru fiecare număr întreg $ n $. În această topologie, punctele izolate $ n $ nu sunt mulțimi închise, deoarece nu pot fi obținute ca complementară a unui ansamblu deschis.
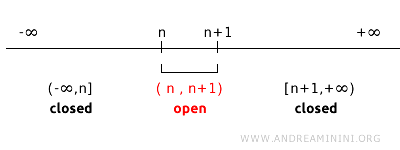
exemplu de topologie generată de intervale
De exemplu, mulțimile $ (1,2) $ și $ (2,3) $ sunt deschise în această topologie. Complementara lui $ (1,2) $ este $ (-\infty, 1] \cup [2, +\infty) $, iar cea a lui $ (2,3) $ este $ (-\infty, 2] \cup [3, +\infty) $.

Observăm că nu există niciun ansamblu deschis a cărui complementară să fie exact $\{2\}$. În general, pentru orice mulțime deschisă de forma $ (n, n+1) $, complementara este o reuniune de intervale închise, $ (-\infty, n] \cup [n+1, +\infty) $. Așadar, în această topologie, punctele izolate $ n $ nu sunt închise, ceea ce evidențiază faptul că noțiunea de „mulțime închisă” depinde în mod esențial de topologia aleasă.

Observații suplimentare

Câteva aspecte importante merită subliniate:

Mulțimi închise și puncte de acumulare
Un punct de acumulare al unei mulțimi este un punct pentru care orice vecinaj, oricât de mic, conține întotdeauna cel puțin un alt punct al mulțimii. Această proprietate este fundamental legată de mulțimile închise, deoarece o mulțime este închisă dacă include toți punctele sale de acumulare.

Exemplu: Considerăm intervalul închis $[0,1]$ pe dreapta reală. El conține toate punctele sale de acumulare.

Punctul $0{,}5$, de pildă, are orice vecinaj deschis plin de alte puncte ale intervalului, ceea ce confirmă statutul său de punct de acumulare.
exemplu de punct de acumulare în [0,1]

Același fenomen se observă și la extremitățile intervalului. De exemplu, punctul $0$ este un punct de acumulare al mulțimii $[0,1]$, deoarece orice vecinaj conține alte puncte ale intervalului, precum $0{,}1$, $0{,}01$, $0{,}001$ etc.
puncte de acumulare la extremitățile intervalului [0,1]
Așadar, toate punctele intervalului $[0,1]$ sunt puncte de acumulare ale acestuia.

O mulțime $ A $ este închisă dacă și numai dacă $ A = \overline{A} $
Într-un spațiu topologic, o mulțime $ A $ este închisă atunci când coincide cu propria sa închidere, adică $ A = \overline{A} $. Închiderea lui $ A $, notată $ \overline{A} $, include atât punctele mulțimii, cât și punctele de acumulare. Prin urmare, o mulțime este închisă dacă reține toate punctele sale de acumulare.

Aceste observații oferă o perspectivă mai amplă asupra conceptului de mulțime închisă și a modului în care acesta depinde de topologia considerată.