Spațiile simplu conexe în topologie

În topologie, spunem că un spațiu este simplu conex atunci când orice drum închis din interiorul său poate fi „strâns” treptat până devine un singur punct, fără ca traseul să iasă din acel spațiu.

Mai simplu spus, un spațiu este simplu conex dacă orice buclă desenată în el se poate contracta complet, ca și cum am trage ușor de un elastic până dispare într-un punct.

Asta înseamnă că spațiul este un întreg unitar, fără găuri sau rupturi interne - un fel de suprafață continuă și „fără fisuri”.

Notă : orice spațiu simplu conex este, desigur, și un spațiu conex. Dar nu toate spațiile conexe sunt simplu conexe - există conexe care ascund „capcane” topologice, cum ar fi găurile.

Un exemplu ușor de înțeles

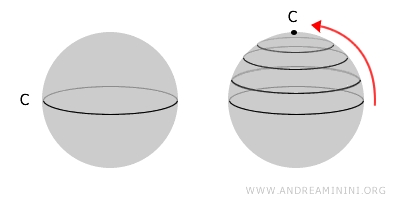
Imaginează-ți o sferă. Dacă trasezi o buclă oriunde pe ea, poți micșora acea buclă pas cu pas până când se transformă într-un singur punct. De aceea, sfera este un spațiu simplu conex.

Lucrurile se schimbă însă dacă vorbim despre un tor - forma clasică de „gogoașă”. Acesta are un gol central, iar unele bucle care trec prin acel gol nu pot fi reduse la un punct fără a „rupe” spațiul. De aceea, torul nu este simplu conex.

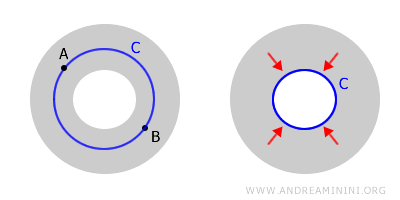
Exemplul arată clar diferența: conexitatea nu garantează și o simplă conexitate.

„Gogoașa” este conexă, pentru că orice două puncte pot fi unite printr-un drum care rămâne în interior. Totuși, nu toate buclele de pe suprafața ei pot fi contractate complet.

În astfel de situații, spunem că spațiul este multiplu conex. Exemple familiare sunt regiunea inelară sau spațiul troidal - ambele conțin „goluri” care complică topologia.

Pe scurt, simpla conexitate este o proprietate mai puternică decât conexitatea prin arce: doar spațiile fără goluri o îndeplinesc pe deplin.