Conexitatea în topologie

În topologie, spunem că un spațiu este conex atunci când nu poate fi împărțit în două regiuni complet separate. Mai simplu spus, conexitatea indică dacă orice două puncte ale unui spațiu pot fi unite printr-un drum continuu, fără a ieși din interiorul acestuia.

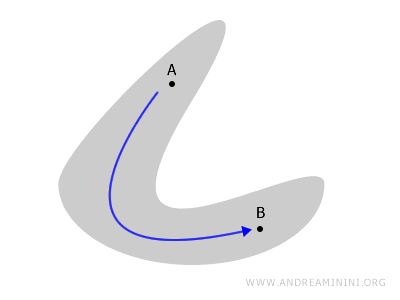
Conexitatea descrie gradul de „unitate” al unui spațiu topologic, adică dacă toate părțile sale comunică între ele sau dacă există separări care rup legătura dintre regiuni.

Este o proprietate topologică fundamentală, deoarece este definită exclusiv în termeni de mulțimi deschise.

De asemenea, este un concept de bază în topologie, strâns legat de ideea de continuitate.

În matematică, noțiunea de conexitate ne ajută să înțelegem structura internă a unui spațiu, modul în care componentele sale sunt legate și relaționează între ele. Din acest motiv, conexitatea joacă un rol esențial în clasificarea și studiul spațiilor topologice.

Un exemplu intuitiv

Imaginați-vă un spațiu, de exemplu o suprafață plană sau un obiect tridimensional. Acesta este conex dacă putem merge de la orice punct A la orice punct B urmând un drum continuu care rămâne în întregime în interiorul spațiului.

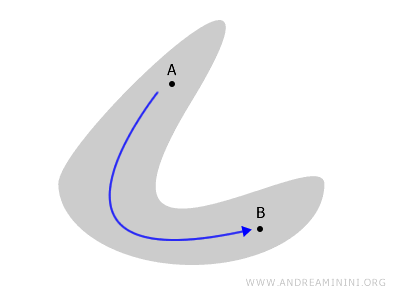
Dacă însă anumite regiuni sunt izolate unele de altele, spațiul nu mai este conex. În acest caz, vorbim despre un spațiu neconex.

De exemplu, dacă spațiul este împărțit în două părți care nu se ating, orice drum între punctele A și B ar trebui să iasă din spațiu.

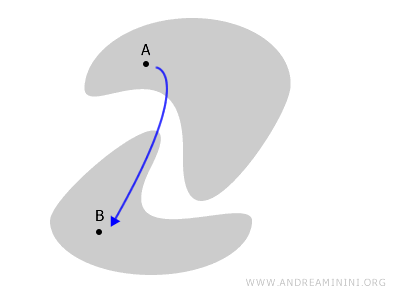
Când un spațiu nu este conex?

O analogie simplă este cea a două camere separate într-o clădire, despărțite de un perete. Fiecare cameră poate fi considerată o mulțime deschisă, iar peretele, care le separă, nu face parte din spațiul analizat.

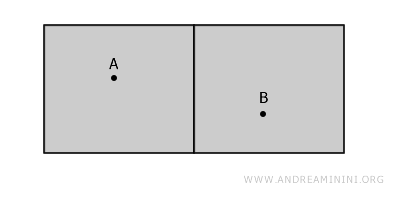
Chiar dacă cele două camere sunt apropiate fizic, ele nu sunt conexe, deoarece orice drum de la A la B ar trebui să traverseze peretele, adică o zonă care nu aparține spațiului.

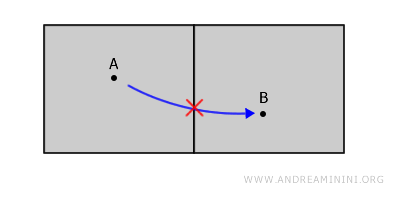
Este important de reținut că, în topologie, frontierele nu fac parte din mulțimile deschise. Acest detaliu are consecințe esențiale asupra modului în care sunt definite și clasificate spațiile.

Conexitatea locală

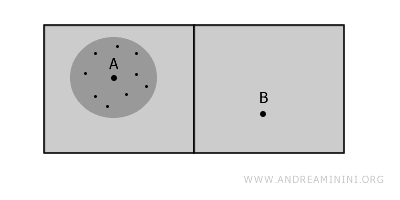
Conexitatea locală apare atunci când fiecare punct al unui spațiu are în jurul său o vecinătate care este, la rândul ei, conexă. Astfel, chiar dacă spațiul global este format din părți separate, fiecare componentă rămâne conexă la scară locală.

Revenind la exemplul celor două camere, ele formează împreună un spațiu neconex, deoarece nu putem trece dintr-una în cealaltă fără a traversa pereții.

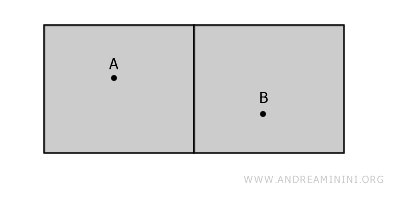
Totuși, în interiorul fiecărei camere, oricare două puncte pot fi unite printr-un drum continuu, ceea ce înseamnă că fiecare componentă este local conexă.

Tipuri de conexitate

Există mai multe forme de conexitate, dintre care cele mai importante sunt următoarele:

• Conexitatea topologică
  Un spațiu topologic $ X $ se numește conex dacă nu poate fi scris ca reuniunea a două mulțimi deschise, disjuncte și nevidente. Cu alte cuvinte, nu există o separare a spațiului în două regiuni independente.

  Exemplu. Intervalul (-1, 1) este conex, în timp ce mulțimea (-1, 0) ∪ (0, 1) nu este conexă, deoarece există două mulțimi deschise, disjuncte și nevidente, (-1, 0) și (0, 1), a căror reuniune acoperă întregul spațiu. Acestea constituie o separație a spațiului.

• Conexitatea prin drumuri (sau prin arcuri)
  Un spațiu topologic este conex prin drumuri dacă pentru orice două puncte A și B există un drum continuu care le unește și rămâne în întregime în interiorul spațiului. Orice spațiu conex prin drumuri este conex, însă reciproca nu este valabilă în general.

  De exemplu, într-o figură plană închisă, orice două puncte interioare pot fi unite printr-o curbă continuă, fără a ieși din conturul figurii.
  
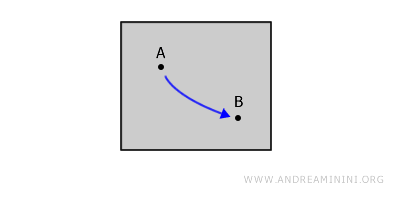
  Diferența dintre conexitatea prin arcuri și cea prin drumuri.  În cazul conexității prin arcuri, drumul trebuie să fie injectiv, adică să nu se intersecteze și să nu treacă de mai multe ori prin același punct.

• Conexitatea simplă
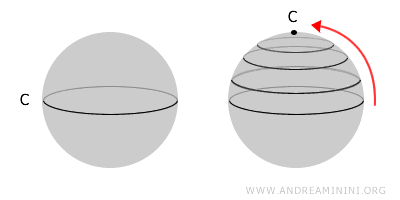
  Un spațiu este simplu conex dacă orice buclă închisă din interiorul său poate fi contractată continuu până la un punct, fără a părăsi spațiul. Aceasta înseamnă că spațiul nu conține „găuri” topologice.

  De exemplu, o sferă este un spațiu simplu conex, deoarece orice buclă trasată pe suprafața sa poate fi micșorată până devine un punct. În schimb, un tor conține un gol central, iar unele bucle nu pot fi contractate. Prin urmare, torul este conex, dar nu simplu conex.
  
  
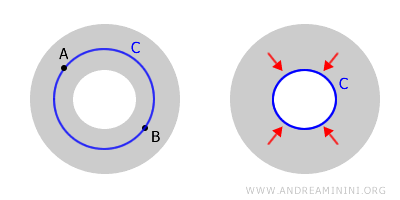
  Un spațiu conex, dar nu simplu conex, se numește spațiu multiplu conex. Un inel este un exemplu clasic al unei astfel de structuri.

De reținut

• În cazul numerelor reale, singurele spații conexe sunt intervalele.

Conexitatea este mai mult decât o noțiune abstractă. Ea oferă o descriere elegantă a unității și continuității formelor și joacă un rol central atât în topologie, cât și în aplicațiile sale din geometrie și fizică.