Spații conexe prin arce

Un spațiu topologic S se numește conex prin arce atunci când orice două puncte A și B din interiorul său pot fi unite printr-o cale continuă, fără a părăsi spațiul respectiv.

Imaginați-vă o simplă coală de hârtie, fără margini. Este o suprafață continuă, deschisă, care nu include limitele exterioare.

Pe această foaie puteți uni oricare două puncte A și B desenând o linie neîntreruptă, fără a ridica creionul de pe hârtie. Linia rămâne mereu în interiorul foii - exact aceasta este ideea de conexiune prin arce.

Cu alte cuvinte, o cale continuă care unește două puncte nu iese niciodată din spațiul care le conține.

Orice spațiu conex prin arce este și un spațiu conex.

Intuitiv, este ușor de înțeles de ce: dacă spațiul ar fi format din părți separate, nu am putea trasa nicio linie continuă între două puncte fără a trece dintr-o parte în alta, adică fără a părăsi spațiul.

Totuși, inversul nu este întotdeauna adevărat. Există spații care sunt conexe, dar nu sunt conexe prin arce.

Iată un exemplu celebru și aparent paradoxal, dar perfect valid.

Să considerăm două mulțimi, Q și T:

$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$

$$ T = \{ \ 0 \} $$

Mulțimea Q conține toate punctele graficului funcției sinus definite pentru toate valorile reale, mai puțin pentru x=0, unde expresia nu este definită (deoarece implică împărțirea la zero).

Mulțimea T reprezintă pur și simplu punctul zero.

Aceste două mulțimi, Q și T, sunt infinit de apropiate una de cealaltă. Dacă urmăriți graficul funcției sin(1/x), veți observa că oscilațiile devin tot mai dese pe măsură ce ne apropiem de zero.

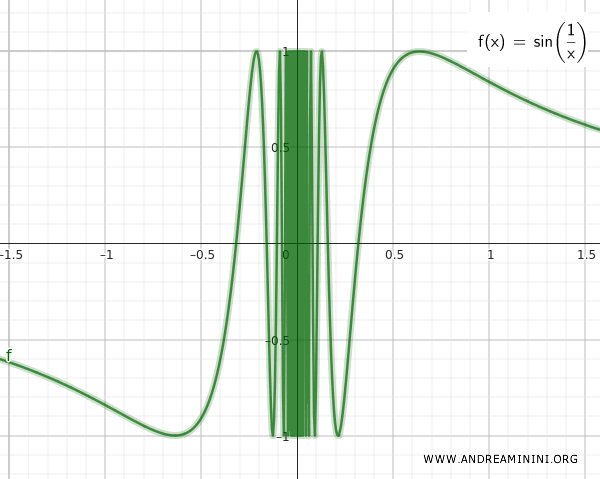
Reunind cele două mulțimi obținem:

$$ S = Q \cup T $$

Mulțimea S este conexă, pentru că oricât de mic ar fi intervalul din jurul lui zero (0-ε, 0+ε), acesta conține întotdeauna puncte aparținând lui Q.

Asta se întâmplă deoarece zero este un punct de acumulare al funcției sin(1/x).

Totuși, S nu este conexă prin arce: nu există nicio cale continuă care să unească un punct din Q cu punctul zero din T fără a ieși din mulțime. În apropierea lui zero, oscilațiile funcției devin atât de dese încât nu pot fi parcurse printr-o singură linie continuă.

Notă: Dacă am lua funcția f(x)=1/x, situația ar fi complet diferită. În acest caz, mulțimile Q și T sunt clar separate, fără nicio apropiere infinită.

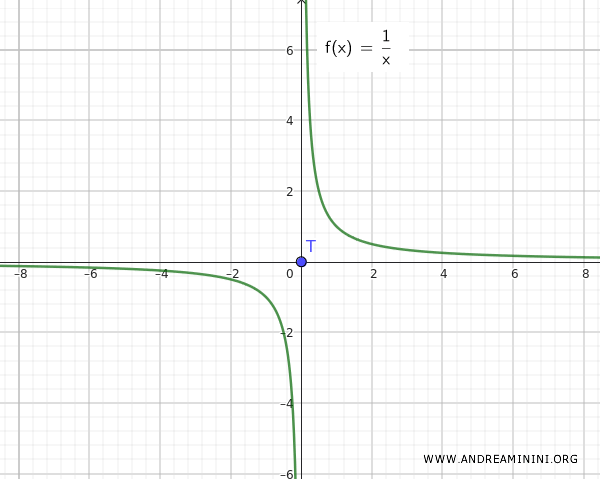
Acest exemplu arată că reuniunea unei mulțimi conexe Q={∀ x ∈ R-{0}, 1/x} și a unui punct izolat T={0} nu este neapărat o mulțime conexă. Pentru a fi conexă, punctul izolat (zero, în acest caz) trebuie să fie și un punct de acumulare.

 Astfel de exemple ne ajută să înțelegem mai profund diferența subtilă dintre conexiunea simplă și conexiunea prin arce în topologie.