Spațiul conex în topologie

Ce înseamnă „a fi conex” într-un spațiu topologic

Pe scurt, un spațiu este topologic conex atunci când nu poate fi împărțit în două regiuni deschise complet separate. Dacă putem face o astfel de separare, spațiul este disconex, iar perechea $(U, V)$ poartă numele de separare a lui $(X)$.

Notă. Aceasta este definiția formală a conexității topologice. Ea diferă de alte noțiuni, cum ar fi „conexitatea prin drumuri” sau „prin arce”. Vom vedea mai jos că cele două concepte nu sunt întotdeauna echivalente.

Un exemplu simplu și intuitiv

Să luăm o mulțime cu doar trei puncte:

$$ X = {a, b, c} $$

Putem defini două topologii posibile pe această mulțime:

• Topologia A
  $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$
• Topologia B
  $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$

Care dintre cele două spații este conex?

Ne amintim regula: un spațiu este conex dacă nu există două mulțimi deschise, nevidente și disjuncte, a căror reuniune să acopere întregul spațiu.

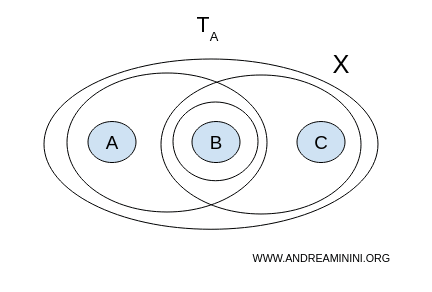
1] Topologia A

Verificăm dacă putem găsi o separare $(U, V)$ în $ \mathcal{T}_A $:

• $ U = {a,b}, V = {b,c} $ - nu sunt disjuncte (ambele conțin $ b $);
• $ U = {a,b}, V = {b} $ - nu sunt disjuncte;
• $ U = {b}, V = {b,c} $ - din nou, nu sunt disjuncte.

Nicio pereche potrivită. Așadar, în topologia A, spațiul $ X $ este conex.

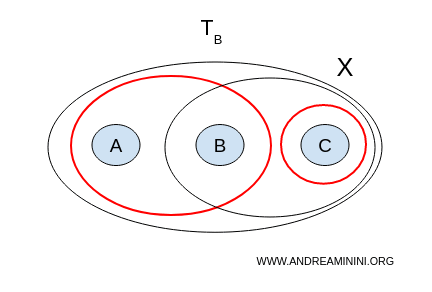
2] Topologia B

În schimb, pentru topologia $ \mathcal{T}_B $:

• $ U = {a,b}, V = {b,c} $ - nu sunt disjuncte;
• $ U = {a,b}, V = {c} $ - sunt disjuncte, nevidente și $ U \cup V = X $.

Avem o separare validă. Prin urmare, în topologia B, spațiul $ X $ este disconex.

Notă. Observați că aceeași mulțime de puncte poate fi fie conexă, fie disconexă, în funcție de topologia aleasă. Așadar, conexitatea nu depinde doar de „puncte”, ci și de structura topologică impusă asupra lor.

Un exemplu pe dreapta reală

Să analizăm acum un caz mai familiar. Fie spațiul:

$$ X = (-\infty, n) \cup (n, +\infty) $$

unde $ n $ este un număr real fix (de exemplu $ n = 0 $). Este dreapta reală din care am eliminat un punct:

$$ X = \mathbb{R} \setminus {n} $$

Verificăm proprietățile:

• $ U = (-\infty, n) $ și $ V = (n, +\infty) $ sunt deschise în topologia standard pe $ \mathbb{R} $;
• sunt disjuncte (nu au puncte comune);
• sunt nevidente;
• iar $ U \cup V = X $.

Rezultă că spațiul $ X $ este disconex, deoarece poate fi împărțit în două regiuni deschise, separate complet una de alta.

Notă. Eliminarea unui singur punct „rupe” continuitatea dreptei reale: obținem două ramuri distincte, una la stânga și una la dreapta lui $ n $, care nu pot fi unite printr-o cale continuă. De aceea, spațiul este nu doar disconex, ci și neconex prin drumuri.

Conex vs. conex prin drumuri

Este important să facem distincția între conexitatea topologică și conexitatea prin drumuri.

• Conexitate topologică: spațiul nu poate fi împărțit în două mulțimi deschise, disjuncte și nevidente, a căror reuniune este întregul spațiu.
• Conexitate prin drumuri: pentru orice două puncte din spațiu, există o cale continuă care le unește, fără a părăsi spațiul. Dacă această cale nu se intersectează cu ea însăși, spațiul este numit conex prin arce.

Pe scurt: toate spațiile conexe prin drumuri sunt conexe, dar nu toate spațiile conexe sunt și conexe prin drumuri.

O cale continuă între două puncte împiedică „tăierea” spațiului în regiuni deschise separate, dar absența unei astfel de căi nu implică neapărat discontinuitate topologică.

Exemplu celebru. Curba sinusului topologului este un caz fascinant: $$ S = { (x, \sin(1/x)) \mid x > 0 } \cup { (0, y) \mid -1 \le y \le 1 } $$ Acest spațiu este conex (nu poate fi împărțit în două regiuni deschise disjuncte), dar nu este conex prin drumuri, deoarece nu există o cale continuă care să lege un punct de pe curba oscilantă de unul de pe segmentul vertical.

Conexitatea, așadar, nu este doar o proprietate abstractă: ea descrie cât de „unitar” este un spațiu - dacă poate fi spart sau dacă rămâne, în sens topologic, un întreg inseparabil.

Note

Câteva precizări suplimentare privind noțiunea de spațiu conex

• Teoremă: caracterizarea spațiilor conexe prin mulțimile deschise și închise (clopen)
  Un spațiu topologic \( X \) este conex dacă și numai dacă singurele sale submulțimi care sunt simultan deschise și închise (clopen) sunt întregul spațiu \( X \) și mulțimea vidă \( \emptyset \). Acest criteriu oferă o modalitate directă și elegantă de a stabili dacă un spațiu poate fi descompus în submulțimi disjuncte sau dacă, dimpotrivă, constituie un întreg coerent și inseparabil.

Numeroase alte rezultate și exemple dezvoltă această idee și arată că noțiunea de conexitate reprezintă una dintre proprietățile structurale esențiale ale spațiilor topologice.