Teoremă: caracterizarea spațiilor conexe prin mulțimile deschise și închise

Un spațiu topologic \( X \) se numește conex dacă și numai dacă singurele sale submulțimi care sunt simultan deschise și închise (denumite clopen) sunt întregul spațiu \( X \) și mulțimea vidă \( \emptyset \).

Altfel spus, un spațiu este conex atunci când nu poate fi reprezentat ca reuniunea a două submulțimi deschise, disjuncte și nevides. Într-un astfel de caz, singurele mulțimi clopen existente sunt cele două cazuri triviale: întregul spațiu și mulțimea vidă.

Acest rezultat constituie un criteriu fundamental al conexității topologice, permițând determinarea caracterului conex al unui spațiu fără a recurge la concepte mai avansate, cum ar fi conexitatea prin arce.

Interpretare teoretică

În topologie, o submulțime care este simultan deschisă și închisă determină o separare a spațiului, adică o descompunere a lui \( X \) în două submulțimi deschise, disjuncte și nevides.

Dacă o astfel de submulțime există, atunci spațiul poate fi scris ca reuniunea a două mulțimi deschise, disjuncte și nevides, și este prin urmare neconex (numit și disconex în unele lucrări).

În schimb, dacă singurele mulțimi clopen din \( X \) sunt \( X \) și \( \emptyset \), nu există nicio separare topologică posibilă, iar spațiul \( X \) este conex.

Observație. În orice spațiu topologic, întregul spațiu \( X \) și mulțimea vidă \( \emptyset \) sunt întotdeauna atât deschise, cât și închise. Acestea reprezintă cele două cazuri triviale de mulțimi clopen.

Exemplul 1: un spațiu finit neconex

Considerăm \( X = \{ a, b, c, d \} \) dotat cu topologia \( T \), definită prin mulțimile deschise \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \).

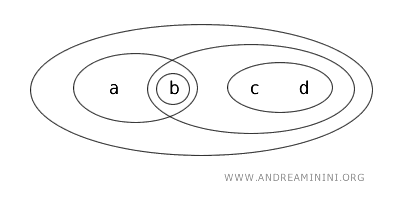
În acest caz, submulțimea \( \{ a, b \} \) este clopen, deoarece:

• este deschisă, întrucât aparține explicit familiei de mulțimi deschise a topologiei \( T \);
• este închisă, deoarece complementara sa \( X \setminus \{ a, b \} = \{ c, d \} \) este, la rândul ei, o mulțime deschisă din \( T \).

Rezultă că spațiul topologic \( (X, T) \) este neconex, deoarece conține o submulțime proprie, nevidă, care este clopen.

Existența unei singure mulțimi clopen netriviale este suficientă pentru a demonstra că un spațiu topologic nu este conex.

Într-adevăr, prezența unei asemenea mulțimi arată că spațiul poate fi exprimat ca reuniunea a două mulțimi deschise, disjuncte și nevides, \( \{ a, b \} \) și \( \{ c, d \} \). Prin urmare, condiția de conexitate topologică nu este îndeplinită.

Exemplul 2: dreapta reală

Considerăm mulțimea numerelor reale \( \mathbb{R} \), dotată cu topologia standard (sau topologia uzuală), generată de intervalele deschise \( (a, b) \).

În această topologie, intervalele \( (a, b) \) sunt mulțimi deschise dar nu sunt închise, în timp ce intervalele închise \( [a, b] \) sunt închise dar nu sunt deschise.

Singurele submulțimi ale lui \( \mathbb{R} \) care sunt simultan deschise și închise sunt \( \mathbb{R} \) și \( \emptyset \).

Prin urmare, dreapta reală, echipată cu topologia standard, este un spațiu conex.

Exemplul 3: un subspațiu neconex al lui \( \mathbb{R} \)

Considerăm subspațiul \( X = (0,1) \cup (2,3) \subset \mathbb{R} \), dotat cu topologia indusă de topologia standard a lui \( \mathbb{R} \).

În această topologie, intervalele \( (0,1) \) și \( (2,3) \) sunt simultan deschise și închise în \( X \), deoarece complementara fiecăruia în \( X \) este exact celălalt interval. Mai precis:

• complementara lui \( (0,1) \) în \( X \) este \( (2,3) \), care este deschisă în \( X \);
• complementara lui \( (2,3) \) în \( X \) este \( (0,1) \), de asemenea deschisă în \( X \).

Prin urmare, ambele submulțimi sunt clopen.

Existența acestor submulțimi netriviale, care sunt simultan deschise și închise, arată că subspațiul \( X \) este neconex.

Cu alte cuvinte, \( X \) este compus din două componente conexe distincte, \( (0,1) \) și \( (2,3) \), care sunt deschise, disjuncte și nevides. Imposibilitatea de a conecta un punct dintr-o componentă cu un punct din cealaltă printr-o curbă continuă exprimă exact lipsa conexității topologice.