Separarea unui subansamblu cu ajutorul mulțimilor deschise
Fie \( A \) un subansamblu al unui spațiu topologic \( X \). Spunem că mulțimile deschise \( U \) și \( V \) din \( X \) separă acest subansamblu atunci când sunt îndeplinite trei condiții de bază, bine cunoscute în topologie:
- Acoperă complet ansamblul \( A \) \[ A \subseteq U \cup V \]
- Fiecare dintre ele întâlnește \( A \) într-un mod nevid \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
- Nu împart niciun punct al lui \( A \) \[ U \cap V \cap A = \varnothing \]
Cu aceste condiții, \( A \) se împarte în două regiuni distincte, fiecare situată într-una dintre mulțimile deschise. Ideea este simplă: dacă un punct din \( A \) ar aparține simultan lui \( U \) și lui \( V \), atunci nu am mai putea vorbi de o separare reală.
Acesta este modul standard în care topologia descrie structuri care pot fi împărțite în două componente prin intermediul deschiselor.
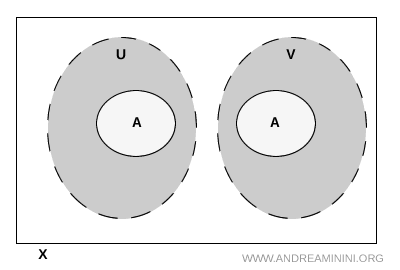
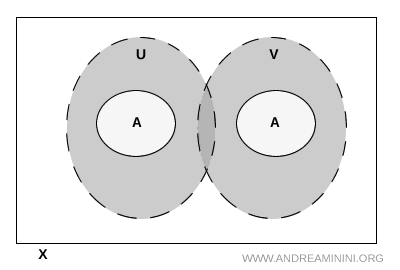
Nota. Chiar dacă \( U \) și \( V \) se pot intersecta în alte zone ale spațiului \( X \), acest lucru nu afectează separarea lui \( A \). Important este ca intersecția lor să nu conțină puncte din subansamblu.
Un exemplu pentru a clarifica ideea
Considerăm \( X = \mathbb{R} \), cu topologia sa obișnuită, și analizăm subansamblul:
$$ A = [-2,-1] \cup [1,2] $$
Acest ansamblu este format din două intervale închise, complet separate.
Definim două mulțimi deschise familiare:
$$ U = (-3,0) $$
$$ V = (0,3) $$
Iată reprezentarea lor pe axa reală:
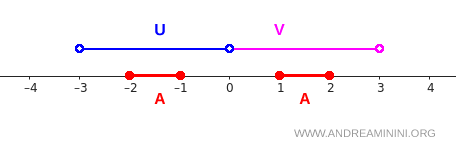
Intervalul \( [-2,-1] \) se află în întregime în \( U \), iar intervalul \( [1,2] \) este complet în \( V \). Totul se aliniază exact cu ceea ce cere definiția.
Într-adevăr:
$$ A \subseteq U \cup V $$
Ambele deschise întâlnesc subansamblul:
$$ U \cap A = [-2,-1] \neq \varnothing $$
$$ V \cap A = [1,2] \neq \varnothing $$
Iar intersecția lor cu \( A \) este vidă:
$$ U \cap V \cap A = \varnothing $$
Astfel, \( U \) și \( V \) formează o separare clară a subansamblului \( A \) în spațiul topologic \( X \).