Orice submulțime conexă este inclusă într-o unică componentă conexă
Fie \( A \) și \( B \) două submulțimi ale unui spațiu topologic \( X \). Presupunem că \( A \) este conexă și că \( A \subset B \). Dacă mulțimea \( B \) poate fi separată în două submulțimi disjuncte \( B_1 \) și \( B_2 \) în spațiul \( X \), atunci \( A \) trebuie, în mod necesar, să fie inclusă în întregime într-una dintre acestea: $$ A \subset B_1 \quad \text{sau} \quad A \subset B_2 $$
Spus mai simplu, o submulțime conexă nu poate „trece" dintr-o parte în alta a unei separări. Ea nu poate intersecta simultan ambele componente.
De fiecare dată când o submulțime conexă se află într-o mulțime care se descompune în două părți disjuncte, ea nu se poate distribui între ele. Este obligată să rămână integral într-una singură dintre părți.
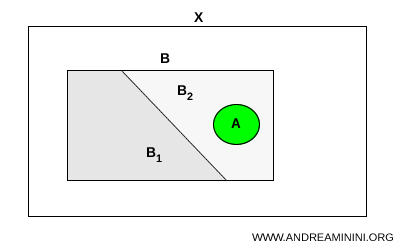
O analogie intuitivă ajută mult. Putem vedea o submulțime conexă ca pe o frânghie continuă aflată într-un înveliș. Dacă învelișul este împărțit în două compartimente complet separate, iar frânghia rămâne întreagă, ea nu poate ajunge decât într-unul dintre ele. Pentru a ocupa ambele compartimente, frânghia ar trebui ruptă. Exact această imposibilitate este surprinsă de noțiunea de conexitate.
Un exemplu concret
Să lucrăm într-un spațiu familiar:
$$ X = \mathbb{R} $$
și să considerăm submulțimea:
$$ B = (-3,4) $$
Această mulțime se poate separa natural în două submulțimi:
$$ B_1 = (-3,0) $$
$$ B_2 = (0,4) $$
Ele sunt disjuncte:
$$ B_1 \cap B_2 = \varnothing $$
iar reuniunea lor reconstruiește exact mulțimea inițială:
$$ B_1 \cup B_2 = B $$
În plus, ambele sunt deschise în topologia de subspațiu indusă pe \( B \), deci formează o separare a lui \( B \) în spațiul \( X \).
Să considerăm acum o submulțime conexă a lui \( B \):
$$ A = (1,2) $$
Este imediat clar că \( A \subset B_2 \). Submulțimea \( A \) este, așadar, conținută complet într-una dintre cele două părți ale separării, exact așa cum afirmă rezultatul general.
Observație. Dacă am lua în schimb \( A = (-1,1) \), am obține $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ O asemenea situație nu este posibilă, deoarece \( B_1 \) și \( B_2 \) formează o separare a lui \( B \). O submulțime conexă nu poate fi „împărțită" între cele două părți. Dacă acest lucru s-ar întâmpla, atunci \( A \) ar admite la rândul său o separare, ceea ce ar contrazice faptul fundamental că intervalul \( (-1,1) \) este conex. Ideea-cheie nu este pierderea conexității intervalului, ci imposibilitatea ca acesta să fie inclus într-o mulțime separată în acest mod.
Demonstrație
Ipoteze
Fie \( A \) și \( B \) submulțimi ale unui spațiu topologic \( X \):
$$ A \subset X \quad \text{și} \quad B \subset X $$
Presupunem că:
- \( A \) este conexă
- \( A \subset B \)
- \( B_1 \) și \( B_2 \) formează o separare a lui \( B \) în spațiul \( X \)
Propoziție
În aceste condiții, submulțimea \( A \) este inclusă fie în \( B_1 \), fie în \( B_2 \):
$$ A \subset B_1 \quad \text{sau} \quad A \subset B_2 $$
Demonstrație
Deoarece \( B_1 \) și \( B_2 \) constituie o separare a lui \( B \), avem:
- \( B_1 \cap B_2 = \varnothing \)
- \( B = B_1 \cup B_2 \)
- \( B_1 \) și \( B_2 \) sunt deschise în topologia de subspațiu indusă pe \( B \)
Să presupunem, pentru a ajunge la o contradicție, că \( A \) nu este inclusă complet nici în \( B_1 \), nici în \( B_2 \). Atunci:
$$ A \cap B_1 \neq \varnothing \qquad \text{și} \qquad A \cap B_2 \neq \varnothing $$
Deoarece \( A \subset B \), putem scrie:
$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$
Mulțimile \( A \cap B_1 \) și \( A \cap B_2 \) sunt disjuncte, deoarece \( B_1 \) și \( B_2 \) sunt disjuncte.
Mai mult, fiindcă \( B_1 \) și \( B_2 \) sunt deschise în \( B \), intersecțiile \( A \cap B_1 \) și \( A \cap B_2 \) sunt deschise în topologia de subspațiu indusă pe \( A \).
Rezultă astfel două submulțimi nevidente, disjuncte și deschise ale lui \( A \), care formează o separare a lui \( A \). Acest lucru contrazice ipoteza că \( A \) este conexă.
Prin urmare, presupunerea inițială este falsă și concluzia corectă este:
$$ A \subset B_1 \quad \text{sau} \quad A \subset B_2 $$
Propoziția este astfel demonstrată.
Și așa mai departe.