Criteriu de conexitate prin intersecție nevidă

Fie \( C_1, C_2, \dots, C_n \subset X \) submulțimi conexe ale unui spațiu topologic \( X \), astfel încât intersecția lor să fie nevidă: \[
\bigcap_{i=1}^n C_i \neq \varnothing . \] În această situație, reuniunea lor \( \bigcup_{i=1}^n C_i \) este, la rândul ei, un ansamblu conex.

Cu alte cuvinte, dacă mai multe mulțimi conexe au cel puțin un punct comun, ele formează împreună o structură care rămâne conexă.

Ideea este simplă, dar esențială: existența unui punct comun împiedică „ruperea” mulțimii în două părți separate.

Observație. Condiția \( \bigcap_{i=1}^n C_i \neq \varnothing \) este suficientă pentru a garanta conexitatea reuniunii \( \bigcup_{i=1}^n C_i \), dar nu este obligatorie. Există situații în care o reuniune de mulțimi conexe rămâne conexă chiar dacă nu există un punct comun tuturor. Acest lucru se întâmplă, de exemplu, atunci când mulțimile se suprapun treptat sau sunt legate printr-un lanț de intersecții succesive.

Un exemplu concret

Să considerăm următoarele submulțimi ale planului \( \mathbb{R}^2 \):

• \( C_1 \): segmentul orizontal care unește punctele \( (-1,0) \) și \( (1,0) \);
• \( C_2 \): segmentul vertical care unește punctele \( (0,-1) \) și \( (0,1) \);
• \( C_3 \): segmentul diagonal care unește punctele \( (-1,-1) \) și \( (1,1) \).

Fiecare dintre aceste mulțimi este conexă.

În plus, toate au un punct comun, și anume \( (0,0) \):

\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]

Prin urmare, intersecția lor este nevidă:

\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]

Conform criteriului prezentat mai sus, reuniunea acestor mulțimi este un ansamblu conex:

\[ C_1 \cup C_2 \cup C_3 \]

Cele trei segmente se întâlnesc într-un punct central comun, ceea ce garantează conexitatea reuniunii lor.

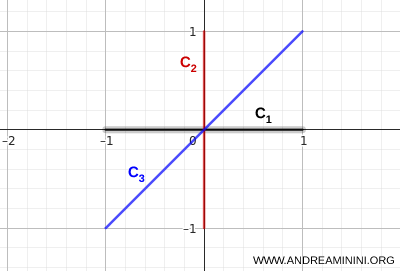
Din orice punct al unuia dintre segmente se poate ajunge în orice alt punct fără a părăsi reuniunea.

Observație. Există și alte criterii de conexitate care nu presupun existența unui punct comun tuturor mulțimilor. De exemplu, dacă mulțimile \( C_i \) sunt conexe și se intersectează succesiv, adică dacă \( C_i \cap C_{i+1} \neq \varnothing \), atunci reuniunea lor \( \bigcup_i C_i \) este conexă, chiar dacă \( \bigcap_i C_i = \varnothing \). Totuși, nici această condiție nu este necesară. Reuniunea poate rămâne conexă chiar și atunci când unele perechi succesive sunt disjuncte, atâta timp cât alte mulțimi asigură legătura. Un exemplu clasic este cel al celor trei segmente care formează un triunghi. Deși intersecția lor globală este vidă, \( \bigcap_i C_i = \varnothing \), reuniunea lor rămâne conexă.

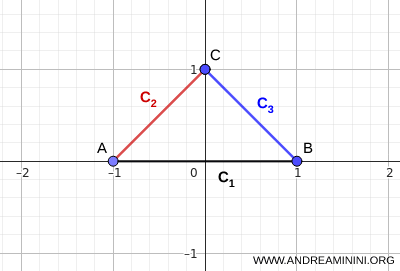
Acest exemplu arată clar că noțiunea de conexitate poate rezulta dintr-o structură de intersecții locale.

Demonstrație

Fie \( X \) un spațiu topologic și fie \( \{C_i\}_{i \in I} \) o familie de submulțimi conexe ale lui \( X \), a căror intersecție este nevidă:

\[ \bigcap_{i \in I} C_i \neq \varnothing \]

Să presupunem, prin reducere la absurd, că reuniunea

\[ C = \bigcup_{i \in I} C_i \]

nu este conexă.

Atunci există două mulțimi deschise \( U \) și \( V \) care formează o separare a lui \( C \), adică:

• \( U \cap C \neq \varnothing \)
• \( V \cap C \neq \varnothing \)
• \( (U \cap C) \cap (V \cap C) = \varnothing \)
• \( C = (U \cap C) \cup (V \cap C) \)

Deoarece intersecția mulțimilor \( C_i \) este nevidă, există un punct

\[ x \in \bigcap_{i \in I} C_i \]

Acest punct aparține tuturor mulțimilor \( C_i \) și, în particular, lui \( C \). El aparține în mod necesar fie lui \( U \), fie lui \( V \), dar nu ambelor, deoarece acestea formează o separare a lui \( C \). Fără a pierde generalitatea, presupunem că

\[ x \in U \quad \text{și} \quad x \notin V \]

Deoarece fiecare \( C_i \) este inclus în \( C \), rezultă că:

\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]

Mulțimile \( C_i \cap U \) și \( C_i \cap V \) sunt deschise în topologia indusă pe \( C_i \), sunt disjuncte, iar reuniunea lor coincide cu \( C_i \). Însă fiecare \( C_i \) este conex, deci una dintre aceste două mulțimi trebuie să fie vidă.

Rezultă că fiecare \( C_i \) este inclusă în întregime fie în \( U \), fie în \( V \).

Deoarece \( x \in C_i \) și \( x \in U \), este imposibil ca \( C_i \subset V \). Prin urmare:

\[ C_i \subset U \quad \text{pentru orice } i \in I \]

În consecință, reuniunea \( C \) este inclusă în \( U \):

\[ \bigcup_{i \in I} C_i \subset U \]

Aceasta contrazice ipoteza conform căreia \( V \cap C \neq \varnothing \).

Contradicția arată că ipoteza inițială este falsă. Concluzionăm astfel că reuniunea \( \bigcup_{i \in I} C_i \) este un ansamblu conex.

Prin urmare, criteriul de conexitate prin intersecție nevidă este demonstrat.