Mulțimi Clopen

O mulțime este numită « clopen » atunci când, în topologia dată, este simultan deschisă și închisă.

Cu alte cuvinte, o mulțime clopen îndeplinește în paralel condițiile specifice celor două noțiuni fundamentale din topologie: mulțime deschisă și mulțime închisă. Denumirea « clopen » provine din îmbinarea cuvintelor englezești « closed » și « open ».

Aceste mulțimi sunt importante deoarece reunesc proprietățile a două clase aparent opuse. Ele apar rar în topologia obișnuită de pe mulțimea numerelor reale, însă sunt frecvente în alte spații topologice, unde oferă indicii esențiale despre structura spațiului.

O mulțime este clopen exact atunci când atât ea, cât și complementara ei sunt deschise în aceeași topologie.

Un Exemplu Concret

Considerăm mulțimea \(X=\{a,b,c,d\}\) împreună cu o topologie \(T\).

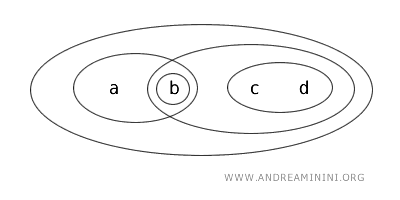
În topologia \(T\), mulțimile deschise sunt: \(\{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, \{a,b,c,d\}, \varnothing\).

Rezultă că submulțimea \(\{a,b\}\) este o mulțime deschisă în această topologie.

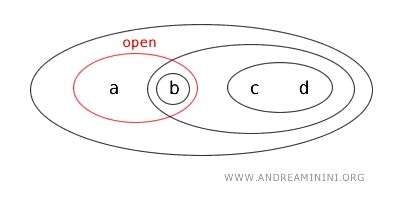
Observăm însă că \(\{a,b\}\) este în același timp și complementara mulțimii deschise \(\{c,d\}\) :

$$ X - \{ c,d \} = \{a , b \} $$

Iar complementara unei mulțimi deschise este mereu o mulțime închisă.

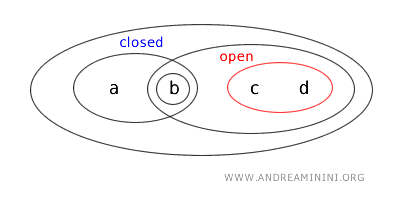
Prin urmare, \(\{a,b\}\) este simultan deschisă și închisă, deci este o mulțime clopen.

De ce sunt importante mulțimile Clopen

Mulțimile clopen joacă un rol esențial în identificarea componentelor topologice ale unui spațiu. Ele indică o separare internă a spațiului, fără granițe la nivel topologic. Studierea lor ajută la înțelegerea structurii interne și a gradului de conectivitate al spațiului analizat.

Două Cazuri Speciale: Mulțimea Vidă și Întregul Spațiu

În orice topologie pe o mulțime \(X\), atât mulțimea vidă (\(\varnothing\)), cât și întregul spațiu (\(X\)) sunt întotdeauna clopen.

Acest lucru reiese direct din definiții: ambele sunt deschise prin axiomă, iar o mulțime este închisă atunci când complementara ei este deschisă. Complementara lui \(X\) este \(\varnothing\), iar complementara lui \(\varnothing\) este \(X\). Prin urmare, ambele sunt închise și, implicit, clopen.

În concluzie, mulțimile clopen reprezintă un instrument fundamental în analiza topologică. Ele pot părea la început o raritate sau o curiozitate teoretică, dar în multe tipuri de spații devin un punct-cheie în înțelegerea structurii globale.

Acest concept va reapărea în mod natural în studiul conexității și al decompozării topologice, unde rolul mulțimilor clopen devine central.