Homeomorfisme în topologie

Un homeomorfism este o transformare topologică definită printr-o funcție care este în același timp bijectivă și continuă, având inversa sa tot continuă.

Spus mai plastic, un homeomorfism permite transformarea continuă a unui spațiu într-altul și revenirea la forma inițială fără rupturi, lipituri sau discontinuități.

Pe scurt, un homeomorfism descrie o trecere lină și reversibilă între două spații, fără modificarea structurii lor fundamentale.

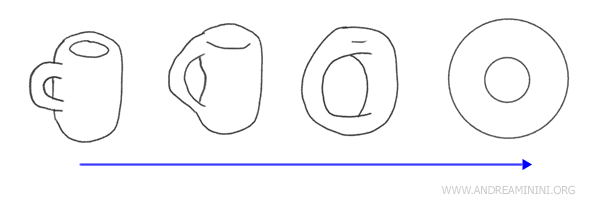
Să luăm ca exemplu o ceașcă de cafea cu toartă și o gogoașă (tor). Aceste două obiecte sunt homeomorfe din punct de vedere topologic, deoarece pot fi deformate continuu unul în celălalt, fără a rupe sau a adăuga părți noi.

Din perspectivă topologică, cele două forme sunt echivalente, ambele având un singur „gol”: orificiul central al gogoșii și spațiul toartei ceștii. Putem modela ceașca în jurul toartei pentru a obține forma unei gogoși.

Atunci când două spații topologice sunt legate printr-un homeomorfism, ele se numesc „spații homeomorfe”. Aceasta înseamnă că, din punct de vedere topologic, sunt identice în esență, chiar dacă formele lor geometrice pot diferi semnificativ.

Proprietățile unui homeomorfism

Iată câteva proprietăți esențiale care caracterizează un homeomorfism:

• Aplicație bijectivă
  Fiecare element al unui spațiu corespunde unui element unic din celălalt spațiu și invers.
• Continuitate
  În mod natural, un homeomorfism este o aplicație continuă: variații mici ale datelor de intrare determină variații mici ale rezultatelor.
• Aplicație inversă continuă
  Inversa aplicației trebuie să fie și ea continuă, ceea ce asigură reversibilitatea transformării fără întreruperea continuității.
• Păstrarea proprietăților topologice
  Un homeomorfism conservă proprietățile topologice fundamentale, precum continuitatea, conexitatea și compacitatea. Astfel, structura internă a spațiului inițial rămâne neschimbată în spațiul rezultat.

Prin urmare, un homeomorfism este o aplicație continuă și bijectivă între două spații topologice \(X\) și \(Y\), a cărei inversă este de asemenea continuă. În acest fel se păstrează proprietățile topologice ale celor două spații.

Simplificat, un homeomorfism permite „reconfigurarea” unui spațiu într-altul fără a-l rupe sau lipi: reprezintă o formă de echivalență topologică perfectă între două structuri spațiale.

Să ne amintim definiția topologică a continuității:

Fie \(X\) și \(Y\) două spații topologice. O aplicație \(f : X \to Y\) se numește continuă dacă, pentru orice mulțime deschisă \(V\) din \(Y\), imaginea inversă \(f^{-1}(V)\) este o mulțime deschisă în \(X\).

Cu alte cuvinte, o aplicație continuă în topologie păstrează structura mulțimilor deschise atunci când trecem dintr-un spațiu în altul.

Noțiunea de continuitate în topologie este mai generală și mai abstractă decât cea utilizată în analiza matematică.

Observație : În analiză, continuitatea depinde de distanța dintre puncte. În topologie, ea se bazează exclusiv pe structura mulțimilor deschise, fără referință la distanță.

Un exemplu concret

Să ilustrăm într-un mod clar și intuitiv conceptele de continuitate și homeomorfism, folosind mulțimi deschise.

Considerăm două spații topologice: \(X = \{a, b, c, d\}\) și \(Y = \{1, 2\}\).

• În spațiul \(X\), mulțimile deschise sunt: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
• În spațiul \(Y\), mulțimile deschise sunt: \(\{\}, \{1\}, \{1, 2\}\).

O aplicație \(f : X \to Y\) este continuă dacă, pentru fiecare mulțime deschisă din \(Y\), imaginea sa inversă este o mulțime deschisă în \(X\).

Definim aplicația \(f\) astfel:

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).

Pentru o înțelegere mai intuitivă, putem reprezenta aplicația \(f\) și structura topologică a fiecărui spațiu, marcând mulțimile deschise prin cercuri.

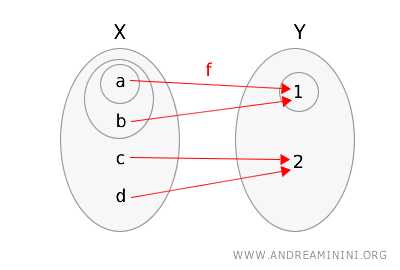
Verificăm acum condiția de continuitate:

• Mulțimea deschisă \(\{1\}\) din \(Y\) are imaginea inversă \(f^{-1}(\{1\}) = \{a, b\}\), care este deschisă în \(X\).
• Mulțimea deschisă \(\{1, 2\}\) din \(Y\) are imaginea inversă \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\), care este de asemenea deschisă în \(X\).

Deoarece imaginea inversă a fiecărei mulțimi deschise din \(Y\) este deschisă în \(X\), aplicația \(f\) este continuă.

Observație : Mulțimea vidă nu este analizată separat, deoarece, prin definiție, este deschisă în orice spațiu topologic.

Să considerăm acum o altă aplicație \(g : X \to Y\), definită prin:

\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\).

Vom reprezenta și această aplicație, indicând mulțimile deschise din fiecare spațiu.

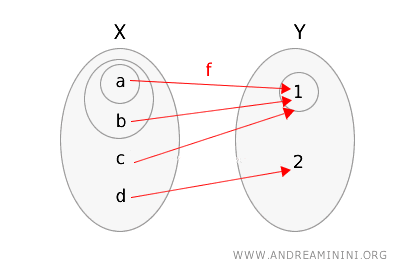
Verificăm continuitatea:

• Mulțimea deschisă \(\{1\}\) din \(Y\) are imaginea inversă \(g^{-1}(\{1\}) = \{a, b, c\}\), care nu este deschisă în \(X\).

Deoarece există o mulțime deschisă în \(Y\) a cărei imagine inversă nu este deschisă în \(X\), aplicația \(g\) nu este continuă.

Observație : În concluzie, o aplicație este continuă dacă imaginea inversă a oricărei mulțimi deschise din spațiul de sosire (\(Y\)) este o mulțime deschisă în spațiul de plecare (\(X\)). În primul exemplu, funcția \(f\) este continuă deoarece îndeplinește această condiție pentru toate mulțimile deschise. În schimb, funcția \(g\) nu o îndeplinește pentru toate cazurile.

Definiția unui homeomorfism

Fie două spații topologice \( X \) și \( Y \) și o aplicație bijectivă \( f : X \to Y \) care are o inversă \( f^{-1} : Y \to X \). Dacă atât \( f \), cât și \( f^{-1} \) sunt continue, atunci \( f \) se numește homeomorfism, iar spațiile \( X \) și \( Y \) sunt homeomorfe, adică \( X \cong Y \).

Astfel de spații se numesc și echivalente din punct de vedere topologic.

Ce înseamnă concret acest lucru?

Două spații sunt homeomorfe - sau topologic echivalente - atunci când posedă aceeași structură fundamentală din punct de vedere topologic, chiar dacă formele lor geometrice pot fi complet diferite.

Un homeomorfism se definește prin trei condiții esențiale:

1. Bijectivitate - Aplicația \( f : X \to Y \) este atât injectivă, cât și surjectivă. Cu alte cuvinte, fiecărui punct din \( X \) îi corespunde un punct unic din \( Y \), și invers.
2. Continuitatea lui \( f \) - Aplicația este continuă dacă imaginea inversă a oricărei mulțimi deschise din \( Y \) este o mulțime deschisă în \( X \).
3. Continuitatea lui \( f^{-1} \) - Inversa \( f^{-1} : Y \to X \) trebuie să fie, la rândul ei, continuă, adică imaginea inversă a oricărei mulțimi deschise din \( X \) este o mulțime deschisă în \( Y \).

Exemplu: Imaginați-vă o foaie de hârtie care este rulată pentru a forma un cilindru. Cilindrul și foaia plană sunt homeomorfe, deoarece putem trece de la unul la celălalt fără a tăia sau lipi - este suficient să rulăm sau să derulăm. Deși formele lor geometrice diferă, structura lor topologică (adică organizarea mulțimilor deschise) rămâne neschimbată.

Este esențial de remarcat că faptul că o aplicație bijectivă \( f \) este continuă nu garantează continuitatea inversului \( f^{-1} \), cu excepția cazului în care \( f \) este și o aplicație deschisă.

Cu alte cuvinte, o funcție continuă și bijectivă nu este neapărat un homeomorfism dacă inversa sa nu este continuă.

În topologie, spunem că o aplicație \( f : X \to Y \) este continuă dacă imaginea inversă a oricărei mulțimi deschise din \( Y \) este o mulțime deschisă în \( X \).

Totuși, acest fapt nu implică automat că imaginea directă a unei mulțimi deschise din \( X \) este și ea deschisă în \( Y \).

Pentru ca \( f^{-1} \) să fie continuă, este necesar ca \( f \) să fie nu doar continuă și bijectivă, ci și o aplicație deschisă.

Exemplu

Considerăm următoarele spații topologice:

• \( X = (a, b) \), cu topologia \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
• \( Y = (1, 2) \), cu topologia \( T_Y = \{\emptyset, Y\} \).

Definim aplicația \( f : X \to Y \) astfel: \( f(a) = 1 \), \( f(b) = 2 \).

Aplicația este evident bijectivă: fiecărui element din \( X \) îi corespunde un element unic din \( Y \), și reciproc.

Observație: În diagramă, mulțimile deschise sunt indicate prin cercuri. În \( X \), mulțimile \{a\}, \{b\} și \{a, b\} sunt deschise; în \( Y \), doar \{1, 2\} este deschisă. Mulțimile vide, deschise prin definiție, nu sunt reprezentate.

Să analizăm acum continuitatea lui \( f \) și a inversului său \( f^{-1} \).

• Continuitatea lui \( f \)
  Topologia \( T_Y \) conține doar \( \emptyset \) și \( Y \). Avem:
  • \( f^{-1}(\emptyset) = \emptyset \), deschisă în \( T_X \)
  • \( f^{-1}(Y) = X \), deschisă în \( T_X \)
  Prin urmare, \( f \) este continuă.
• Continuitatea lui \( f^{-1} \)
  Considerăm acum \( f^{-1} : Y \to X \), cu \( f^{-1}(1) = a \) și \( f^{-1}(2) = b \). Pentru deschisele din \( X \):
  • \( f^{-1}(\emptyset) = \emptyset \), deschisă în \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), care nu este deschisă în \( T_Y \)
  • \( f^{-1}(\{b\}) = \{2\} \), nici aceasta
  • \( f^{-1}(X) = Y \), deschisă în \( T_Y \)
  Deoarece unele imagini inverse nu sunt deschise, \( f^{-1} \) nu este continuă.

Prin urmare, deși \( f \) este bijectivă și continuă, inversa sa nu este. Rezultă că \( f \) nu este un homeomorfism.

Acest exemplu arată că simpla continuitate și bijectivitate nu garantează automat continuitatea inversului.

Observație: Lipsa continuității lui \( f^{-1} \) se explică prin diferența dintre topologii: cea a lui \( X \) este mai fină (conține mai multe mulțimi deschise) decât cea a lui \( Y \), care este mai grosieră.

Exemplul 2

Să analizăm acum un alt caz, cu topologii diferite:

• \( X = (a, b) \), cu \( T_X = \{\emptyset, \{a\}, X\} \).
• \( Y = (1, 2) \), cu \( T_Y = \{\emptyset, \{1\}, Y\} \).

Definim \( f : X \to Y \) prin \( f(a) = 1 \), \( f(b) = 2 \).

Aplicația \( f \) este, din nou, bijectivă.

Să verificăm acum continuitatea lui \( f \) și a lui \( f^{-1} \).

• Continuitatea lui \( f \)
  Deschisele din \( Y \) sunt \( \emptyset \), \(\{1\}\) și \( Y \):
  • \( f^{-1}(\emptyset) = \emptyset \), deschisă în \( T_X \)
  • \( f^{-1}(\{1\}) = \{a\} \), deschisă în \( T_X \)
  • \( f^{-1}(Y) = X \), deschisă în \( T_X \)
  Toate imaginile inverse sunt deschise, deci \( f \) este continuă.
• Continuitatea lui \( f^{-1} \)
  Deschisele din \( X \) sunt \( \emptyset \), \(\{a\}\) și \( X \):
  • \( f^{-1}(\emptyset) = \emptyset \), deschisă în \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), deschisă în \( T_Y \)
  • \( f^{-1}(X) = Y \), de asemenea deschisă în \( T_Y \)
  Așadar, inversa \( f^{-1} \) este și ea continuă.

Rezultă că \( f \) este bijectivă, continuă, iar inversa sa este, la rândul ei, continuă. Prin urmare, \( f \) este un homeomorfism.

Diferența față de primul exemplu constă în alegerea topologiilor, care aici sunt mai bine armonizate între ele.

Observație: Acest exemplu arată că, pentru a garanta continuitatea inversului - și, prin urmare, existența unui homeomorfism - este esențial ca topologiile de pe \( X \) și \( Y \) să fie compatibile.

Diferența dintre homeomorfisme și alte transformări topologice

Deși termenul „homeomorfism” este uneori folosit în mod general pentru a desemna transformările topologice, în sens strict el desemnează o categorie particulară a acestora.

Homeomorfismele și transformările topologice sunt concepte înrudite, dar nu identice:

• Transformări topologice
  Acest termen se referă la o clasă largă de aplicații între spații topologice care păstrează anumite proprietăți fundamentale, precum continuitatea, conexitatea sau compacitatea. Această clasă include homeomorfismele, dar și alte tipuri de transformări, cum ar fi izotopiile, homotopiile și difeomorfismele.
• Homeomorfisme
  Acestea sunt aplicații bijective și continue, a căror inversă este, de asemenea, continuă. Ele stabilesc o corespondență perfect reversibilă între două spații, conservând integral structura lor topologică. Două spații legate printr-un homeomorfism sunt, din punct de vedere topologic, indistinguibile, chiar dacă formele lor geometrice pot fi foarte diferite.

În concluzie, orice homeomorfism este o transformare topologică, dar nu orice transformare topologică este un homeomorfism: numai acelea care respectă criteriile de bijectivitate și dublă continuitate.

Există aplicații care, deși păstrează anumite proprietăți topologice esențiale, nu îndeplinesc toate condițiile pentru a fi considerate homeomorfisme.

Observații suplimentare

Iată câteva clarificări utile pentru o mai bună înțelegere a rolului și semnificației homeomorfismelor:

• Proprietate topologică
  O proprietate topologică este o caracteristică intrinsecă a unui spațiu care rămâne neschimbată sub acțiunea unui homeomorfism. Cu alte cuvinte, dacă două spații sunt homeomorfe (legate printr-o aplicație continuă, bijectivă și cu inversă continuă), ele posedă exact aceleași proprietăți topologice.
• Teorema lui Hausdorff privind homeomorfismele
  Această teoremă afirmă că, dacă \( f : X \to Y \) este un homeomorfism și \( X \) este un spațiu Hausdorff, atunci și \( Y \) este Hausdorff. Cu alte cuvinte, homeomorfismele conservă proprietățile topologice, inclusiv proprietatea de separare a punctelor specifică spațiilor Hausdorff.
• Echivalentul noțiunii de homeomorfism în algebră este izomorfismul de grupuri. Dacă un izomorfism conservă structura algebrică a unui obiect, un homeomorfism conservă structura topologică - adică organizarea mulțimilor deschise într-un spațiu.

Și așa mai departe.